题目内容
5. 一质量为m的小球以初动能EK0冲上倾角为θ的粗糙斜面,图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系(以斜面底端为零势能面,h0表示上升的最大高度,图中坐标数据中的k为常数且满足0<k<1),则由图可知,下列结论正确的是( )
一质量为m的小球以初动能EK0冲上倾角为θ的粗糙斜面,图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系(以斜面底端为零势能面,h0表示上升的最大高度,图中坐标数据中的k为常数且满足0<k<1),则由图可知,下列结论正确的是( )| A. | 上升过程中摩擦力大小f=k mgcosθ | |
| B. | 上升过程中摩擦力大小f=k mgsinθ | |
| C. | 上升高度h=$\frac{k+1}{k+2}{h_0}$时,小球重力势能和动能相等 | |
| D. | 上升高度h=$\frac{k+1}{k+2}{h_0}$sinθ时,小球重力势能和动能相等 |
分析 本题要分析动能、重力势能的变化规律以及与高度的关系,抓住:
(1)动能大小的影响因素:EK=$\frac{1}{2}$mv2,质量、速度.质量越大,速度越大,动能越大.
(2)重力势能大小的影响因素:质量、被举得高度.质量越大,高度越高,重力势能越大.
(3)机械能=动能+势能.物体没有发生弹性形变时,不考虑弹性势能.
(4)机械能的减少量数值上等于摩擦力的负功.
解答 解:A、①为重力势能的变化曲线,②为动能的变化曲线,上升过程中机械能的减少量数值上等于摩擦力的负功,h0表示上升的最大高度,故斜面长度为s=$\frac{{h}_{0}}{sinθ}$,由fs=EK0-$\frac{{E}_{K0}}{k+1}$,故f=$\frac{k{E}_{K0}sinθ}{(1+k){h}_{0}}$,而由图象知:mgh0=$\frac{{E}_{K0}}{k+1}$,联立解得:f=kmgsinθ,故A错误,B正确.
C、当上升高度h=$\frac{1+k}{2+k}$h0时,重力势能为mgh=$\frac{1+k}{2+k}$mgh0,由动能定理结合B选项分析得,此时动能为EK′=EK0-f$\frac{h}{sinθ}$-mgh=$\frac{1+k}{2+k}$mgh0,故此时小球重力势能和动能相等,故C正确,D错误.
故选:BC.
点评 掌握动能和重力势能大小的影响因素,根据图象能确定动能和势能的大小.根据“E=EK+EP”计算机械能的大小.根据动能定理分过程求解动能.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
15.在物理学发展过程中,很多科学家做出了巨大的贡献,下列说法中符合史实的是( )
| A. | 伽利略通过观测、分析计算发现了行星的运动规律 | |
| B. | 开普勒利用他精湛的数学经过长期计算分析,最后终于发现了万有引力定律 | |
| C. | 牛顿运用万有引力定律预测并发现了海王星和冥王星 | |
| D. | 卡文迪许用扭秤实验测出了万有引力常量 |
16. 在西昌卫星发射中心由长征三号乙运载火箭携带中国第一艘月球车成功发射,实现了中国首次月面软着陆,假设月球车在月球表面竖直弹射一小球,初速度为v0,经过时间t落回原处,已知月球的平均密度ρ,万有引力常量为G,下列说法正确的是( )
在西昌卫星发射中心由长征三号乙运载火箭携带中国第一艘月球车成功发射,实现了中国首次月面软着陆,假设月球车在月球表面竖直弹射一小球,初速度为v0,经过时间t落回原处,已知月球的平均密度ρ,万有引力常量为G,下列说法正确的是( )
 在西昌卫星发射中心由长征三号乙运载火箭携带中国第一艘月球车成功发射,实现了中国首次月面软着陆,假设月球车在月球表面竖直弹射一小球,初速度为v0,经过时间t落回原处,已知月球的平均密度ρ,万有引力常量为G,下列说法正确的是( )
在西昌卫星发射中心由长征三号乙运载火箭携带中国第一艘月球车成功发射,实现了中国首次月面软着陆,假设月球车在月球表面竖直弹射一小球,初速度为v0,经过时间t落回原处,已知月球的平均密度ρ,万有引力常量为G,下列说法正确的是( )| A. | 月球表面处的重力加速度是$\frac{{v}_{0}}{t}$ | |
| B. | 月球的半径是$\frac{3{v}_{0}}{2πρGt}$ | |
| C. | 月球的质量是$\frac{{9v}_{0}^{3}}{2{π}^{2}{ρ}^{2}{G}^{3}{t}^{3}}$ | |
| D. | 月球的第一宇宙速度是$\frac{{v}_{0}}{t}$$\sqrt{\frac{6}{πρG}}$ |
13.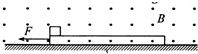 如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )
如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )
 如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )
如图所示,空间有一垂直纸面向外的磁感应强度为0.5T的匀强磁场,一质量为0.2kg且足够长的绝缘木板静止在光滑水平面上,在木板左端无初速放置一质量为0.1㎏、电荷量q=+0.2C的滑块,滑块与绝缘木板之间的动摩擦因数为0.5,滑块受到的最大静摩擦力可认为等于滑动摩擦力.现对木板施加方向水平向左,大小为0.6N的恒力,g取10m/s2.则( )| A. | 木板和滑块一直做加速度为2m/s2的匀加速运动 | |
| B. | 滑块开始做匀加速运动,然后做匀速直线运动 | |
| C. | 最终木板做加速度为2m/s2的匀加速运动,滑块做速度为10m/s的匀速运动 | |
| D. | 最终木板做加速度为3m/s2的匀加速运动,滑块做速度为10m/s的匀速运动 |
17.关于机械能守恒定律的适用条件,下列说法中正确的是( )
| A. | 当物体只有重力作功时,机械能一定守恒 | |
| B. | 当物体做自由落体运动时(不计空气阻力),机械能一定守恒 | |
| C. | 当物体做平抛运动时(不计空气阻力),机械能一定守恒 | |
| D. | 当物体做斜上抛运动时(不计空气阻力),机械能一定守恒 |
14.下列说法正确的是( )
| A. | 回复力一定是振动物体所受的合外力 | |
| B. | 弹簧振子振动过程中,速度增大时,加速度一定减小 | |
| C. | 声波与观察者相互接近时,波源发出的声波的频率会升高 | |
| D. | 由波长、波速和频率的关系v=λf可知,波源频率越高,波的传播速度越大 |
15.如图,a、b、c是在地球大气层外圆形轨道上运行的三颗人造地球卫星,下列说法中正确的是( )

| A. | b、c的线速度大小相等,且小于a的线速度 | |
| B. | b、c的向心加速度大小相等,且大于a的向心加速度 | |
| C. | c加速(速率增大)可追上同一轨道上的b | |
| D. | b、c周期相等,且大于a的周期 |
 如图,足够长的木板质量M=10kg,放置于光滑水平地面上,以初速度vo=5m/s沿水平地面向右匀速运动现有足够多的小铁块,它们的质量均为m=l kg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时.将一小铁块贴着挡板无初速地放在木板上,小铁块与木板的上表面间的动摩擦因数μ=0.5.当木板运动了L=1m时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块.只要木板运动了L就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=l0m/s2).试问:
如图,足够长的木板质量M=10kg,放置于光滑水平地面上,以初速度vo=5m/s沿水平地面向右匀速运动现有足够多的小铁块,它们的质量均为m=l kg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时.将一小铁块贴着挡板无初速地放在木板上,小铁块与木板的上表面间的动摩擦因数μ=0.5.当木板运动了L=1m时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块.只要木板运动了L就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=l0m/s2).试问: