题目内容
15. 如图所示,足够长的斜面倾角θ=37°,一物体以v0=24m/s的初速度从斜面上A点处沿斜面向上运动;加速度大小为a=8m/s2,g取10m/s2,sin37°=0.6,cos37°=0.8,则物体沿斜面上滑的最大距离x=36m,物体与斜面间的动摩擦因数μ=0.25.
如图所示,足够长的斜面倾角θ=37°,一物体以v0=24m/s的初速度从斜面上A点处沿斜面向上运动;加速度大小为a=8m/s2,g取10m/s2,sin37°=0.6,cos37°=0.8,则物体沿斜面上滑的最大距离x=36m,物体与斜面间的动摩擦因数μ=0.25.
分析 (1)根据匀变速直线运动的速度位移公式求出物体沿斜面上滑的最大距离.
(2)根据牛顿第二定律,结合沿斜面方向上产生加速度,垂直斜面方向上合力为零,求出动摩擦因数的大小.
解答 解:(1)由运动学公式得:
$x=\frac{{v}_{0}^{2}}{2a}$=$\frac{2{4}^{2}}{2×8}$=36m
(2)由牛顿第二定律得有:
沿斜面方向上:mgsinθ+f=ma…(1)
垂直斜面方向上:mgcosθ-N=0…(2)
又:f=μN…(3)
由(1)(2)(3)得:μ=0.25
故答案为:36m.0.25.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
5.如图所示的两种电路中,电源相同,电源内阻不计,各电阻器阻值相等,各电流表的内阻相等且不可忽略不计.电流表A1、A2、A3和A4读出的电流值分别为I1、I2、I3和I4.下列关系式中正确的是( )
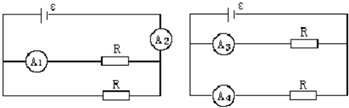

| A. | I1=I3 | B. | I1>I4 | C. | I2=2I1 | D. | I2<I3+I4 |
3.已知万有引力常量为G,下列各组数据可以计算地球质量的是( )
| A. | 月球绕地球运行的周期和运行的半径 | |
| B. | 地球的公转周期和公转轨道半径 | |
| C. | 人造卫星绕地球运行的周期和线速度 | |
| D. | 地球表面的重力加速度和地球的半径 |
10.关于电动势,下列说法错误的是( )
| A. | 电动势的单位是伏特 | |
| B. | 不同的电源的电动势一般是相等的 | |
| C. | 电动势的大小等于没有接入位外电路时电源两端的电压 | |
| D. | 电动势的大小由电源本身的性质来决定 |
20. 如图为“高车踢碗”的杂技,演员踩着独轮车,头顶着碗,将一只碗扣在一只脚上,将碗踢起,由于碗底与空气的接触面积较大,碗所受的空气阻力不可忽略,碗离开脚后在空中划出一段弧线,正好落在头顶的碗里,对碗从扣在脚上到碗落入头顶碗里的整个过程中( )
如图为“高车踢碗”的杂技,演员踩着独轮车,头顶着碗,将一只碗扣在一只脚上,将碗踢起,由于碗底与空气的接触面积较大,碗所受的空气阻力不可忽略,碗离开脚后在空中划出一段弧线,正好落在头顶的碗里,对碗从扣在脚上到碗落入头顶碗里的整个过程中( )
 如图为“高车踢碗”的杂技,演员踩着独轮车,头顶着碗,将一只碗扣在一只脚上,将碗踢起,由于碗底与空气的接触面积较大,碗所受的空气阻力不可忽略,碗离开脚后在空中划出一段弧线,正好落在头顶的碗里,对碗从扣在脚上到碗落入头顶碗里的整个过程中( )
如图为“高车踢碗”的杂技,演员踩着独轮车,头顶着碗,将一只碗扣在一只脚上,将碗踢起,由于碗底与空气的接触面积较大,碗所受的空气阻力不可忽略,碗离开脚后在空中划出一段弧线,正好落在头顶的碗里,对碗从扣在脚上到碗落入头顶碗里的整个过程中( )| A. | 碗在离开脚后处于完全失重状态 | |
| B. | 碗离开脚后所做的运动是斜抛运动 | |
| C. | 若碗在脱离脚时的速度为v,则碗在脱离脚前的过程中的平均速度一定为$\frac{v}{2}$ | |
| D. | 碗脱离脚的瞬间,脚(踢碗的那部分)的加速度大小一定大于碗的加速度大小 |
7.如图所示,某大剧院的屋顶为半球形,一只小猴在该屋顶向上缓慢爬行,它在向上爬的过程中( )
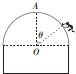

| A. | 屋顶对它的支持力变大 | B. | 屋顶对它的支持力变小 | ||
| C. | 屋顶对它的摩擦力变大 | D. | 屋顶对它的作用力变小 |
4.原子核${\;}_{92}^{235}$U俘获一个慢中子后发生裂变,核反应方程式为:${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+aX,其中X为某种粒子,a为X的个数.则以下说法正确的是( )
| A. | a=3 | |
| B. | x为电子 | |
| C. | 上述原子核中的原子核结合能最大的是${\;}_{92}^{235}$U | |
| D. | 上述原子核中原子核平均结合能最大的是${\;}_{92}^{235}$U |
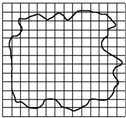 油酸酒精溶液的浓度为每10 000mL油酸酒精溶液中有油酸6mL,用滴管向量筒内滴75滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的单分子油膜的形状如图所示.
油酸酒精溶液的浓度为每10 000mL油酸酒精溶液中有油酸6mL,用滴管向量筒内滴75滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的单分子油膜的形状如图所示.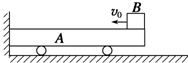 如图所示,一辆质量为M=6kg的平板小车停靠在墙角处,地面水平且光滑,墙与地面垂直.一质量为m=2kg的小铁块(可视为质点)放在平板小车最右端,平板小车上表面水平且与小铁块之间的动摩擦因数μ=0.45,平板小车的长度L=1m.现给铁块一个v0=5m/s的初速度使之向左运动,与竖直墙壁发生弹性碰撞后向右运动,碰撞过程中无能量损失,求小铁块在平板小车上运动的过程中系统损失的机械能(g取10m/s2).
如图所示,一辆质量为M=6kg的平板小车停靠在墙角处,地面水平且光滑,墙与地面垂直.一质量为m=2kg的小铁块(可视为质点)放在平板小车最右端,平板小车上表面水平且与小铁块之间的动摩擦因数μ=0.45,平板小车的长度L=1m.现给铁块一个v0=5m/s的初速度使之向左运动,与竖直墙壁发生弹性碰撞后向右运动,碰撞过程中无能量损失,求小铁块在平板小车上运动的过程中系统损失的机械能(g取10m/s2).