题目内容
5.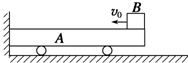 如图所示,一辆质量为M=6kg的平板小车停靠在墙角处,地面水平且光滑,墙与地面垂直.一质量为m=2kg的小铁块(可视为质点)放在平板小车最右端,平板小车上表面水平且与小铁块之间的动摩擦因数μ=0.45,平板小车的长度L=1m.现给铁块一个v0=5m/s的初速度使之向左运动,与竖直墙壁发生弹性碰撞后向右运动,碰撞过程中无能量损失,求小铁块在平板小车上运动的过程中系统损失的机械能(g取10m/s2).
如图所示,一辆质量为M=6kg的平板小车停靠在墙角处,地面水平且光滑,墙与地面垂直.一质量为m=2kg的小铁块(可视为质点)放在平板小车最右端,平板小车上表面水平且与小铁块之间的动摩擦因数μ=0.45,平板小车的长度L=1m.现给铁块一个v0=5m/s的初速度使之向左运动,与竖直墙壁发生弹性碰撞后向右运动,碰撞过程中无能量损失,求小铁块在平板小车上运动的过程中系统损失的机械能(g取10m/s2).
分析 根据动能定理研究铁块向右运动到达竖直墙壁的过程求出到达竖直墙壁时的速度,
铁块在小车上滑动,根据动量守恒定律求出共同速度,再根据功能关系求出小铁块相对小车运动距离进行判断求解.
解答 解:设铁块向右运动到达竖直墙壁时的速度为v1,根据动能定理得:
-μmgL=$\frac{1}{2}$m${v}_{1}^{2}$-$\frac{1}{2}$m${v}_{0}^{2}$
代入数据解得:v1=4m/s
铁块与竖直墙发生弹性碰撞后向右运动,假设小铁块最终和平板车达到共速v2,规定向右为正方向,根据动量守恒定律得:
mv1=(M+m)v2
代入数据解得:v2=1m/s
设小铁块相对小车运动距离x与平板车达到共速,则根据功能关系得:
-μmgx=$\frac{1}{2}$(M+m)${v}_{2}^{2}$-$\frac{1}{2}$m${v}_{1}^{2}$
解得:x=$\frac{4}{3}$m
由于x>L说明铁块在没有与平板车达到共速时就滑出平板车.
所以小铁块在平板上运动过程中系统损失的机械能为:△E=2μmgL=18J.
答:小铁块在平板上运动过程中系统损失的机械能是18J.
点评 本题首先要分析铁块的运动情况,对于铁块向右运动是否滑出平板车,我们可以采用假设法进行判断,正确运用功能关系求解.

练习册系列答案
相关题目
13.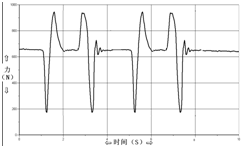 如图所示,是某同学站在力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿),横坐标为时间(单位为秒).由图线可知,该同学的体重约为650N,除此以外,还可以得到以下信息( )
如图所示,是某同学站在力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿),横坐标为时间(单位为秒).由图线可知,该同学的体重约为650N,除此以外,还可以得到以下信息( )
 如图所示,是某同学站在力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿),横坐标为时间(单位为秒).由图线可知,该同学的体重约为650N,除此以外,还可以得到以下信息( )
如图所示,是某同学站在力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿),横坐标为时间(单位为秒).由图线可知,该同学的体重约为650N,除此以外,还可以得到以下信息( )| A. | 该同学做了两次下蹲-起立的动作 | |
| B. | 该同学做了四次下蹲-起立的动作 | |
| C. | 下蹲过程中人经历了失重和超重两种状态 | |
| D. | 起立过程中人处于超重状态 |
10.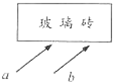 如图所示,两细束平行单色光a,b射向置于空气中的横截面为矩形的玻璃砖的下表面,设玻璃砖足够长.若发现玻璃砖的上表面只有一束光线射出,则下列说法中正确的是 ( )
如图所示,两细束平行单色光a,b射向置于空气中的横截面为矩形的玻璃砖的下表面,设玻璃砖足够长.若发现玻璃砖的上表面只有一束光线射出,则下列说法中正确的是 ( )
 如图所示,两细束平行单色光a,b射向置于空气中的横截面为矩形的玻璃砖的下表面,设玻璃砖足够长.若发现玻璃砖的上表面只有一束光线射出,则下列说法中正确的是 ( )
如图所示,两细束平行单色光a,b射向置于空气中的横截面为矩形的玻璃砖的下表面,设玻璃砖足够长.若发现玻璃砖的上表面只有一束光线射出,则下列说法中正确的是 ( )| A. | 其中有一束单色光在玻璃砖的上表面发生了全反射 | |
| B. | 在玻璃中单色光a的传播速率小于单色光b的传播速率 | |
| C. | 增大光束与玻璃砖下表面间的夹角θ,上表面会有两束平行单色光线射出 | |
| D. | 改变玻璃砖的厚度,a光可能会从b光的右侧射出 | |
| E. | a光的频率大于b光的频率 |
14. 有一种大型娱乐器械可以让人体验超重和失重,其环形座舱套在竖直柱子上,由升降机送上几十米的高处,然后让座舱自由下落.落到一定位置时,制动系统启动,座舱做减速运动,到地面时刚好停下.下列说法中正确的是( )
有一种大型娱乐器械可以让人体验超重和失重,其环形座舱套在竖直柱子上,由升降机送上几十米的高处,然后让座舱自由下落.落到一定位置时,制动系统启动,座舱做减速运动,到地面时刚好停下.下列说法中正确的是( )
 有一种大型娱乐器械可以让人体验超重和失重,其环形座舱套在竖直柱子上,由升降机送上几十米的高处,然后让座舱自由下落.落到一定位置时,制动系统启动,座舱做减速运动,到地面时刚好停下.下列说法中正确的是( )
有一种大型娱乐器械可以让人体验超重和失重,其环形座舱套在竖直柱子上,由升降机送上几十米的高处,然后让座舱自由下落.落到一定位置时,制动系统启动,座舱做减速运动,到地面时刚好停下.下列说法中正确的是( )| A. | 座舱自由下落的过程中人处于超重状态 | |
| B. | 座舱自由下落的过程中人处于失重状态 | |
| C. | 座舱减速下落的过程中人处于失重状态 | |
| D. | 座舱下落的整个过程中人处于超重状态 |
 如图所示,足够长的斜面倾角θ=37°,一物体以v0=24m/s的初速度从斜面上A点处沿斜面向上运动;加速度大小为a=8m/s2,g取10m/s2,sin37°=0.6,cos37°=0.8,则物体沿斜面上滑的最大距离x=36m,物体与斜面间的动摩擦因数μ=0.25.
如图所示,足够长的斜面倾角θ=37°,一物体以v0=24m/s的初速度从斜面上A点处沿斜面向上运动;加速度大小为a=8m/s2,g取10m/s2,sin37°=0.6,cos37°=0.8,则物体沿斜面上滑的最大距离x=36m,物体与斜面间的动摩擦因数μ=0.25.

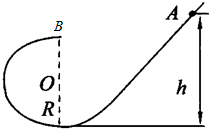 如图所示,光滑轨道顶端高为h,底端通过小段圆弧与半径为R的光滑圆形轨道连接,整个轨道和斜面都在竖直平面内.一个小球从顶端A处由静止释放,通过圆轨道最高点时,对轨道的压力大小等于重力,则斜面高h应该是R的多少倍?
如图所示,光滑轨道顶端高为h,底端通过小段圆弧与半径为R的光滑圆形轨道连接,整个轨道和斜面都在竖直平面内.一个小球从顶端A处由静止释放,通过圆轨道最高点时,对轨道的压力大小等于重力,则斜面高h应该是R的多少倍?