题目内容
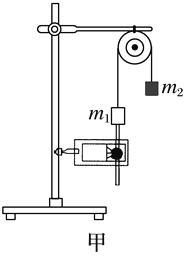
【题目】如图所示，A、B两车相距x=8m时，A车正以vA=5m/s的速度向右匀速运动，而B车此时正以vB=12m/s的初速度向右匀减速运动，加速度a=-2m/s2，求：
（1）A、B两车何时速度相等；
（2）A追上B所经历的时间。
【答案】（1）A、B两车经过3.5s速度相等；（2）A追上B所经历的时间是8.8s。
【解析】
（1）B车的速度为：
vB'=vB+at1
两车速度相等时有：
vB'=vA
解得：
t1=3.5s
（2）A车追上B车时，两车的位移关系为：
xA=x+xB
即：
vAt=x+vBt+
at2
代入数据有：
5t=8+12t+(-2)t2
解得：
t=8s，t=-1s（舍去）
B车做减速运动，设其速度减为0所用的时间为t0，
由速度公式得：
t0=
=6s；
由于t=8s＞t0，所以B车先停下，之后A车才追上B车，
B车的位移为：
xB=vBt0+a
=36m
所以A车追上的时间为：
t2=
代入数据有：
t2=8.8s
练习册系列答案
相关题目
