题目内容
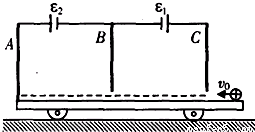
如图所示，三块平行金属板竖直固定在表面光滑的绝缘小车上，A、B板，B、C板间距离均为L，并分别与电动势为ε1和ε2的电池相连，金属板B、C下端开有小孔，两孔的连线沿水平方向垂直于三块金属板，整个装置的总质量为M，并静止在光滑水平面上．现有一质量为m，带电量为+q的小球以初速度v0沿两孔连线方向从C板射入小车（设带电小球不影响板间电场）．（1）小球由C板向B板运动过程中，小球和小车各做什么运动？
（2）证明小球由C板运动到B板的过程中，电场对小球和小车组成的系统所做功为qε1．
（3）为使小球不打到A板上，电动势ε2应满足什么条件？
分析：（1）分析小球和小车的受力情况，判断其运动情况．
（2）金属板B、C间建立匀强电场，其电场强度为EBC=
，带电小球和小车受到的电场力大小为F=qEBC．分别分析电场力对小车和小球做功，确定出电场力做的总功．
（3）当小球与小车相等时，若打不到A板，就打不到A板了，根据系统的动量守恒和功能关系列式求解．
（2）金属板B、C间建立匀强电场，其电场强度为EBC=
| ε1 |
| L |
（3）当小球与小车相等时，若打不到A板，就打不到A板了，根据系统的动量守恒和功能关系列式求解．
解答：解：（1）小球受到水平向左的电场力，则小球向左做匀加速直线运动．根据牛顿第三定律可知，小车受到向右的电场力，小车向右做匀加速直线运动．
（2）金属板B、C间的电场强度为EBC=
带电小球和小车受到的电场力大小为：F=qEBC=
设小车的位移为s，则带电小球的位移为L-s，
电场力对小车做的功为W1=Fs
电场力对带电小球做的功为W2=F（L-s）
所以电场力对带电小球和车组成的系统所做的功为W=W1+W2=FL=qε1．
（3）设带电小球到达A、B板间的D点时相对小车静止，此时带电小球和小车的速度为v，并设B板到D点的电势差为UBD．
由动量守恒，mv0=（M+m）v
由功能关系知：qε1-qUBD=
(M+m)v2-
mv02
解得：UBD=ε1+
所以，要使带电小球不打到A板上，电动势ε2必须满足：ε2＞UBD=ε1+
答：
（1）小球由C板向B板运动过程中，小球向左做匀加速直线运动，小车向右做匀加速直线运动．
（2）证明略．
（3）为使小球不打到A板上，电动势ε2应满足的条件是：?2＞?1+
．
（2）金属板B、C间的电场强度为EBC=
| ε1 |
| L |
带电小球和小车受到的电场力大小为：F=qEBC=
| qε1 |
| L |
设小车的位移为s，则带电小球的位移为L-s，
电场力对小车做的功为W1=Fs
电场力对带电小球做的功为W2=F（L-s）
所以电场力对带电小球和车组成的系统所做的功为W=W1+W2=FL=qε1．
（3）设带电小球到达A、B板间的D点时相对小车静止，此时带电小球和小车的速度为v，并设B板到D点的电势差为UBD．
由动量守恒，mv0=（M+m）v
由功能关系知：qε1-qUBD=
| 1 |
| 2 |
| 1 |
| 2 |
解得：UBD=ε1+
| Mmv02 |
| 2q(M+m) |
所以，要使带电小球不打到A板上，电动势ε2必须满足：ε2＞UBD=ε1+
| Mmv02 |
| 2q(M+m) |
答：
（1）小球由C板向B板运动过程中，小球向左做匀加速直线运动，小车向右做匀加速直线运动．
（2）证明略．
（3）为使小球不打到A板上，电动势ε2应满足的条件是：?2＞?1+
Mm
| ||
| 2q(M+m) |
点评：本题相当于碰撞类型的问题，关键是分析物体的受力情况和运动情况，运用动量守恒和功能关系进行求解．
练习册系列答案
相关题目
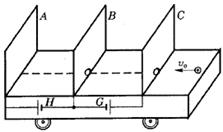如图所示，三块平行金属板竖直固定在表面光滑的绝缘小车上，并与车内的电池连接，小车的总质量为Ｍ，Ａ、Ｂ板，Ｂ、Ｃ板间距均为Ｌ，金属扳Ｂ、Ｃ上，开有小孔，两小孔的连线沿水平方向且垂直于三块金属板，整个装置静止在光滑水平面上，已知车内电池Ｇ的电动势为Ｅ１，电池Ｈ的电动势为Ｅ２，现有一质量为ｍ，带电量为＋ｑ的小球以初速度ｖ０沿两孔连线方向射入小车（设带电小球不影响板间电场）． 
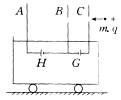如图所示，三块平行金属板竖直固定在绝缘小车上，并与车内电池连接，小车总质量为M，静止在光滑水平面上，金属板B、C中间开有小孔，两孔在同一水平线上，已知车内电池G的电动势为 E1 ，现有一质量为m，带电量为q的粒子(不计重力)，以初速
，水平射入C板小孔，它穿过B板小孔后继续向A板运动。
