题目内容
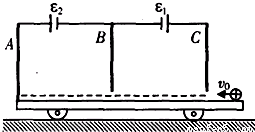
如图所示,三块平行金属板竖直固定在表面光滑的绝缘小车上,A、B板,B、C板间距离均为L,并分别与电动势为E1和E2的电池相连,金属板B、C下端开有小孔,两孔的连线沿水平方向垂直于三块金属板,整个装置的总质量为M,并静止在光滑水平面上。现有一质量为m、带电荷量为+q的小球以初速度v0沿两孔连线方向从C板射入小车(设带电小球不影响板间电场)。
(1)小球由C板向B板运动过程中,小球和小车各做什么运动?
(2)证明小球由C板运动到B板的过程中,电场对小球和小车组成的系统所做功为qε1。
(3)为使小球不打到A板上,电动势ε2应满足什么条件?
解:(1)小球向左做匀加速直线运动,小车向右做匀加速直线运动。(共4分,每答对一项给2分)
(2)金属板B、C间的电场强度为EBC=![]()
带电小球和小车受到的电场力大小为:F=qEBC=![]()
设小车的位移为s,则带电小球的位移为L-s,
电场力对小车做的功为W1=Fs
电场力对带电小球做的功为W2=F(L-s)
所以电场力对带电小球和车组成的系统所做的功为W=W1+W2=FL=qE1。
(3)设带电小球到达A、B板间的D点时相对小车静止,此时带电小球和小车的速度为v,并设B板到D点的电势差为UBD。
由动量守恒,mv0=(M+m)v
由功能关系知:qE1 -qUBD=![]() (M+m)v2-
(M+m)v2-![]()
解得:UBD=E1+![]()
所以,要使带电小球不打到A板上,电动势E2必须满足:
E2>UBD=E1+![]()
(说明:直接由qE1-qE2<![]() (M + m)v2-
(M + m)v2-![]() 。解得结果正确的同样给分)
。解得结果正确的同样给分)
考查带电粒子在电场中的运动,电场力做功,动量守恒定律,功能关系。

练习册系列答案
相关题目
 如图所示,三块平行金属板竖直固定在表面光滑的绝缘小车上,A、B板,B、C板间距离均为L,并分别与电动势为ε1和ε2的电池相连,金属板B、C下端开有小孔,两孔的连线沿水平方向垂直于三块金属板,整个装置的总质量为M,并静止在光滑水平面上.现有一质量为m,带电量为+q的小球以初速度v0沿两孔连线方向从C板射入小车(设带电小球不影响板间电场).
如图所示,三块平行金属板竖直固定在表面光滑的绝缘小车上,A、B板,B、C板间距离均为L,并分别与电动势为ε1和ε2的电池相连,金属板B、C下端开有小孔,两孔的连线沿水平方向垂直于三块金属板,整个装置的总质量为M,并静止在光滑水平面上.现有一质量为m,带电量为+q的小球以初速度v0沿两孔连线方向从C板射入小车(设带电小球不影响板间电场).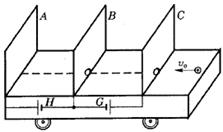 如图所示,三块平行金属板竖直固定在表面光滑的绝缘小车上,并与车内的电池连接,小车的总质量为M,A、B板,B、C板间距均为L,金属扳B、C上,开有小孔,两小孔的连线沿水平方向且垂直于三块金属板,整个装置静止在光滑水平面上,已知车内电池G的电动势为E1,电池H的电动势为E2,现有一质量为m,带电量为+q的小球以初速度v0沿两孔连线方向射入小车(设带电小球不影响板间电场).
如图所示,三块平行金属板竖直固定在表面光滑的绝缘小车上,并与车内的电池连接,小车的总质量为M,A、B板,B、C板间距均为L,金属扳B、C上,开有小孔,两小孔的连线沿水平方向且垂直于三块金属板,整个装置静止在光滑水平面上,已知车内电池G的电动势为E1,电池H的电动势为E2,现有一质量为m,带电量为+q的小球以初速度v0沿两孔连线方向射入小车(设带电小球不影响板间电场). 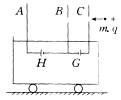 如图所示,三块平行金属板竖直固定在绝缘小车上,并与车内电池连接,小车总质量为M,静止在光滑水平面上,金属板B、C中间开有小孔,两孔在同一水平线上,已知车内电池G的电动势为 E1 ,现有一质量为m,带电量为q的粒子(不计重力),以初速
如图所示,三块平行金属板竖直固定在绝缘小车上,并与车内电池连接,小车总质量为M,静止在光滑水平面上,金属板B、C中间开有小孔,两孔在同一水平线上,已知车内电池G的电动势为 E1 ,现有一质量为m,带电量为q的粒子(不计重力),以初速