题目内容
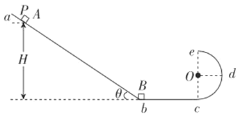
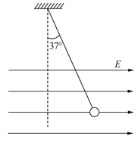
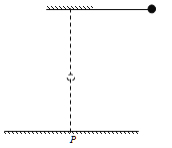
【题目】如图所示，质量为m的小球用长为L的细线拴住，细线所受拉力达到一定值时就会被拉断。现将摆球拉至水平位置而后释放，小球摆到悬点的正下方时细线恰好被拉断。若小球上端悬点到水平地面的高度不变，改变细线的长度L，仍将摆球拉至水平位置后释放，则（P点在悬点的正下方）：（ ）
A.若L变长，小球摆到悬点的正下方时细线可能不会被拉断
B.若L变长，小球落地处到地面上Ｐ点的距离可能不会变长
C.若L变短，小球落地处到地面上Ｐ点的距离一定变短
D.若L变短，小球摆到悬点的正下方时细线一定会被拉断
【答案】BD
【解析】
AD．根据机械能守恒定律可知
最低点由向心力公式可得
解得
与绳长无关，故不论绳子变长还是变短细线均会被拉断，故A错误，D正确；
BC．若L变短，则小球的水平速度变小，但离地高度变大则可知落地时间变长，由平抛运动规律可知
水平位移
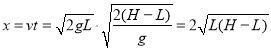
当
时，水平射程最大，则可知L变化时,无法确定射程的变化情况，故B正确，C错误。
故选BD。
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
