题目内容
15. 如图所示,质量mB的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一块质量mA的物块A,一颗质量m0的子弹以v0的水平初速度瞬间射穿A后,速度变为v.已知A与B之间的动摩擦因数不为零,且A与B最终达到相对静止,则系统产生的热量为多少?
如图所示,质量mB的平板车B上表面水平,开始时静止在光滑水平面上,在平板车左端静止着一块质量mA的物块A,一颗质量m0的子弹以v0的水平初速度瞬间射穿A后,速度变为v.已知A与B之间的动摩擦因数不为零,且A与B最终达到相对静止,则系统产生的热量为多少?
分析 子弹射穿物块A的过程、A与B相互作用过程系统定律守恒,应用动量守恒定律求出物体的速度,然后应用能量守恒定律可以求出产生的热量.
解答 解:对于子弹、物块A相互作用过程系统动量守恒,
以子弹的初速度方向为正方向,由动量守恒定律得:m0v0=m0v+mAvA,
对于A、B相互作用过程中,以A的初速度方向为正方向,
由动量守恒定律得:mAvA=(mA+mB)v,
由能量守恒定律得,系统产生的热量:
△E=$\frac{1}{2}$m0v02-$\frac{1}{2}$m0v2-$\frac{1}{2}$(mA+mB)v2,
解得:△E=$\frac{1}{2}$m0v02-$\frac{1}{2}$m0v2-$\frac{{m}_{0}^{2}({v}_{0}-v)^{2}}{2({m}_{A}+{m}_{B})}$;
答:系统产生的热量为:$\frac{1}{2}$m0v02-$\frac{1}{2}$m0v2-$\frac{{m}_{0}^{2}({v}_{0}-v)^{2}}{2({m}_{A}+{m}_{B})}$.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程,应用动量守恒定律与能量守恒定律即可解题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
12. 如图所示,绝綠光滑半圆环轨道固定在空间存在竖直向下的匀强电场和垂直向里的匀强磁场中,电场强度为E,在与环心等高处放且质量为m、带电量为q的小球,由静止开始沿轨道运动,经过环最低点并向左方运动.下述说法正确的是( )
如图所示,绝綠光滑半圆环轨道固定在空间存在竖直向下的匀强电场和垂直向里的匀强磁场中,电场强度为E,在与环心等高处放且质量为m、带电量为q的小球,由静止开始沿轨道运动,经过环最低点并向左方运动.下述说法正确的是( )
 如图所示,绝綠光滑半圆环轨道固定在空间存在竖直向下的匀强电场和垂直向里的匀强磁场中,电场强度为E,在与环心等高处放且质量为m、带电量为q的小球,由静止开始沿轨道运动,经过环最低点并向左方运动.下述说法正确的是( )
如图所示,绝綠光滑半圆环轨道固定在空间存在竖直向下的匀强电场和垂直向里的匀强磁场中,电场强度为E,在与环心等高处放且质量为m、带电量为q的小球,由静止开始沿轨道运动,经过环最低点并向左方运动.下述说法正确的是( )| A. | 该小球一定带正电 | |
| B. | 洛伦兹力对粒子做负功 | |
| C. | 小球经过环的最低点时速度最大 | |
| D. | 小球经过环的最低点时对轨道压力为(mg+Eq) |
13.在下列几种运动中,遵守机械能守恒定律的运动是( )
| A. | 汽车以恒定速率通过拱形桥 | B. | 雨点匀速下落 | ||
| C. | 物体沿光滑斜面下滑 | D. | 汽车刹车的运动 |
3.下列关于向心加速度的说法正确的是( )
| A. | 向心加速度越大,物体速率变化越快 | |
| B. | 向心加速度的方向始终与速度方向垂直 | |
| C. | 在匀速圆周运动中向心加速度是不变的 | |
| D. | 向心加速度的大小与轨道半径成反比 |
20. 如图所示,轻弹簧两端拴接两个小球a、b,拴接小球的细线固定在天花板,两球静止,两细线与水平方向的夹角α=30°,弹簧水平,以下说法正确的是( )
如图所示,轻弹簧两端拴接两个小球a、b,拴接小球的细线固定在天花板,两球静止,两细线与水平方向的夹角α=30°,弹簧水平,以下说法正确的是( )
 如图所示,轻弹簧两端拴接两个小球a、b,拴接小球的细线固定在天花板,两球静止,两细线与水平方向的夹角α=30°,弹簧水平,以下说法正确的是( )
如图所示,轻弹簧两端拴接两个小球a、b,拴接小球的细线固定在天花板,两球静止,两细线与水平方向的夹角α=30°,弹簧水平,以下说法正确的是( )| A. | 两球质量一定相等 | B. | 两球质量可能不相等 | ||
| C. | 剪断左侧细线瞬间,a球加速度为g | D. | 剪断左侧细线瞬间,b球加速度为g |
7.图甲是某小型交流发电机的示意图,两磁极N、S间的磁场可视为水平方向的匀强磁场,线圈绕垂直于磁场方向的水平轴OO′逆时针方向匀速转动,外接电路中A为交流电流表,R为定值电阻,若从图示位置开始计时,电路中产生的交变电流随时间变化的图象如图乙所示,以下判断正确的是( )


| A. | 电流表的示数为20A | |
| B. | 电路中的电流方向每秒钟改变50次 | |
| C. | t=1.5×10-2s时刻穿过线圈的磁通量为零 | |
| D. | 线圈转动的角速度为100πrad/s |
4.一列简谐横波某时刻的波形如图所示,此时质点b的速度方向沿y轴正方向,则( )

| A. | 这列波沿x轴正方向传播 | |
| B. | 再经过一个周期、质点a运动到x=6m处 | |
| C. | 质点f将比质点e先回到平衡位置 | |
| D. | 当质点b运动到最低点时,质点c恰好运动到平衡位置 |
5.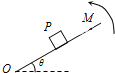 如图,重物P放在粗糙的水平板OM上,当水平板绕O端缓慢抬高,在重物P没有滑动之前,下列说法中正确的是( )
如图,重物P放在粗糙的水平板OM上,当水平板绕O端缓慢抬高,在重物P没有滑动之前,下列说法中正确的是( )
 如图,重物P放在粗糙的水平板OM上,当水平板绕O端缓慢抬高,在重物P没有滑动之前,下列说法中正确的是( )
如图,重物P放在粗糙的水平板OM上,当水平板绕O端缓慢抬高,在重物P没有滑动之前,下列说法中正确的是( )| A. | P受到的支持力做正功 | B. | P受到的支持力不做功 | ||
| C. | P受到的摩擦力做负功 | D. | P受到的摩擦力不做功 |