题目内容
如图所示,竖直放置的光滑圆弧面AB与光滑的凹槽BbcC平滑衔接,CD为光滑的直轨道.质量为m=1kg的小铁块(可视为质点)自圆弧的A点由静止开始滑下,A、B两点的高度差h=0.45m,小铁块运动到B点后水平滑上质量为M=2kg的小车,小车的长度为L=0.65m,小铁块与小车的动摩擦因素µ=0.5,小车的最右端与凹槽右端Cc的水平距离为S=0.7m,小车与凹槽右端Cc碰撞后立刻静止,并与Cc粘合在一起不再分离.g=10m/s2.求(1)小铁块运动到B点的速度大小v
(2)小车与凹槽右端Cc即将碰撞前的速度大小 v
(3)小铁块自静止开始到滑离小车的运动过程中克服摩擦力所做的功Wf.

【答案】分析:(1)小铁块由A运动到B点的过程中,只有重力做功mgh,由动能定理求解小铁块运动到B点的速度大小v.
(2)假设小铁块滑上小车后与小车具有共同速度,根据动量守恒定律求出共同速度,由动能定理分别对铁块和小车进行研究,得到它们的位移,判断速度相等时,小车是否到达凹槽右端和小铁块是否从小车上滑落.再确定小车与凹槽右端Cc即将碰撞前的速度大小v.
(3)分两个过程求克服摩擦力所做的功Wf:小铁块滑上小车到与小车具有共同速度过程和小铁块自静止开始到滑离小车的运动过程.
解答:解:(1)设小铁块由A运动到B点的速度为v,由动能定理有:
mgh=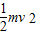
解得:v=3m/s
(2)设小铁块滑上小车后具有共同速度v1,由动量守恒定律有
mv=(M+m)v1
解得:v1=1m/s
在该过程中,设小车的位移为s1,由动能定理有

解得s1=0.2s<s,可知小车还没到达凹槽右端
设小铁块在此过程的位移为s2,由动能定理有

解得 s2=0.8m
小铁块与小车的位移之差△s=s2-s1=0.6m<L,可知小铁块没从小车上滑落.
综合以上分析,小车与凹槽右端Cc端即将碰撞前的速度速度大小v=v1=1m/s.
(3)小铁块滑上小车到与小车具有共同速度过程克服摩擦力做的功为W1,有
W1=μmgs2=4J
从小车与Cc端碰撞到小铁块离开小车的过程中小铁块克服摩擦力做的功为W2,
W2=μmg(L-△s)=0.25J
所以小铁块自静止开始到滑离小车的运动过程中克服摩擦力所做的功
Wf=W1+W2=4.25J
答:
(1)小铁块运动到B点的速度大小v是3m/s.
(2)小车与凹槽右端Cc即将碰撞前的速度大小v是1m/s.
(3)小铁块自静止开始到滑离小车的运动过程中克服摩擦力所做的功Wf是4.25J.
点评:本题是动能定理、动量守恒定律的综合应用,关键是分析铁块与小车速度相同时铁块和凹槽的位置.
(2)假设小铁块滑上小车后与小车具有共同速度,根据动量守恒定律求出共同速度,由动能定理分别对铁块和小车进行研究,得到它们的位移,判断速度相等时,小车是否到达凹槽右端和小铁块是否从小车上滑落.再确定小车与凹槽右端Cc即将碰撞前的速度大小v.
(3)分两个过程求克服摩擦力所做的功Wf:小铁块滑上小车到与小车具有共同速度过程和小铁块自静止开始到滑离小车的运动过程.
解答:解:(1)设小铁块由A运动到B点的速度为v,由动能定理有:
mgh=
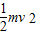
解得:v=3m/s
(2)设小铁块滑上小车后具有共同速度v1,由动量守恒定律有
mv=(M+m)v1
解得:v1=1m/s
在该过程中,设小车的位移为s1,由动能定理有

解得s1=0.2s<s,可知小车还没到达凹槽右端
设小铁块在此过程的位移为s2,由动能定理有

解得 s2=0.8m
小铁块与小车的位移之差△s=s2-s1=0.6m<L,可知小铁块没从小车上滑落.
综合以上分析,小车与凹槽右端Cc端即将碰撞前的速度速度大小v=v1=1m/s.
(3)小铁块滑上小车到与小车具有共同速度过程克服摩擦力做的功为W1,有
W1=μmgs2=4J
从小车与Cc端碰撞到小铁块离开小车的过程中小铁块克服摩擦力做的功为W2,
W2=μmg(L-△s)=0.25J
所以小铁块自静止开始到滑离小车的运动过程中克服摩擦力所做的功
Wf=W1+W2=4.25J
答:
(1)小铁块运动到B点的速度大小v是3m/s.
(2)小车与凹槽右端Cc即将碰撞前的速度大小v是1m/s.
(3)小铁块自静止开始到滑离小车的运动过程中克服摩擦力所做的功Wf是4.25J.
点评:本题是动能定理、动量守恒定律的综合应用,关键是分析铁块与小车速度相同时铁块和凹槽的位置.

练习册系列答案
相关题目
 如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为
如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为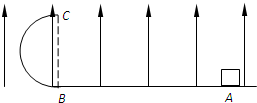 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小 如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )
如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( ) 物理选修3-3
物理选修3-3 如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求
如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求