题目内容
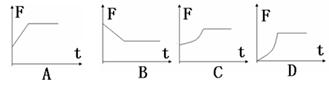
一个弹簧秤放在水平地面上,Q为与轻弹簧上端连在一起的秤盘,P为重物,已知P的质量M ="10.5" kg,Q的质量 m ="1.5" kg,弹簧的质量不计,劲度系数 k ="800" N/m,系统处于静止.如图所示,现给P施加一个方向竖直向上的力F,使它从静止开始向上做匀加速运动,则在向上运动的过程中力F随时间变化的图象是( )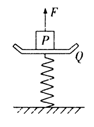
C
解析试题分析: 最初时,弹簧的弹力等于PQ的总重力(M+m)g。
刚开始运动时,PQ的加速度相同,把PQ看成一个整体,PQ整体受到的外力共有3个:重力、向上的力F及弹簧弹力F弹,做匀加速运动,根据牛顿第二定律得:
F合=(M+m)a
F+F弹-(M+m)g=(M+m)a
设P的位移为x
所以F=(M+m)(a+g)-((M+m)g-kx)=(M+m)a+ kat2/2;
即在P与Q分离前F随时间变化图象是抛物线,且t=0时,F=(M+m)a
当P与Q分离时,P只受重力和F作用,仍做匀加速运动,此时F为恒力.故C正确
考点:牛顿第二定律

 全能测控一本好卷系列答案
全能测控一本好卷系列答案如图所示,一根轻弹簧下端固定,竖立在水平面上。其正上方A位置有一只小球。小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零。小球下降阶段下列说法中正确的是: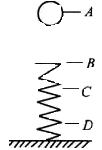
| A.在B位置小球速度最大 |
| B.在C位置小球速度最大 |
| C.从A→C位置小球重力势能的减少量小于重力做的功 |
| D.从A→D位置小球重力势能的减少等于弹簧弹性势能的增加 |
如图所示,在同一竖直平面内有两个正对着的半圆形光滑轨道,轨道的半径都是R.轨道端点所在的水平线相隔一定的距离x.一质量为m的小球能在其间运动而不脱离轨道,经过最低点B时的速度为v.小球在最低点B与最高点A对轨道的压力之差为ΔF(ΔF>0),不计空气阻力.则 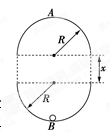
| A.m、x一定时,R越大,ΔF一定越大 |
| B.m、x一定时,v越大,ΔF一定越大 |
| C.m、R一定时,x越大,ΔF一定越大 |
| D.m、R一定时,v越大,ΔF一定越大 |
如图甲所示,用一水平力F拉着一个静止在倾角为(的光滑斜面上的物体,逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图像如图乙所示,g取10m/s2,根据图乙中所提供的信息可以计算出( )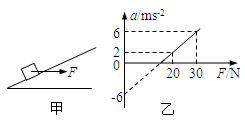
| A.物体的质量 |
| B.斜面的倾角 |
| C.物体能静止在斜面上所施加的最小外力 |
| D.加速度为6 m/s2时物体的速度 |
在升降电梯内的地板上放一体重计,电梯静止时,晓敏同学站在体重计上,体重计示数为50 kg,电梯运动过程中,某一段时间内晓敏同学发现体重计示数如图所示,在这段时间内下列说法中正确的是: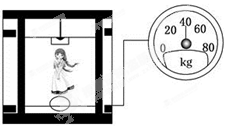
| A.晓敏同学所受的重力变小了 |
| B.晓敏对体重计的压力小于体重计对晓敏的支持力 |
| C.电梯一定在竖直向下运动 |
| D.电梯的加速度大小为g/5,方向一定竖直向下 |
如图甲所示,轻杆一端固定在O点,另一端固定一小球,现让小球在竖直平面内做半径为R的圆周运动。小球运动到最高点时,杆与小球间弹力大小为F,小球在最高点的速度大小为v,其F一v2图象如图乙所示。不计空气阻力,则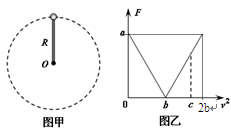
A.小球的质量为 |
B.当地的重力加速度大小为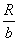 |
| C.v2=c时,杆对小球的弹力方向向下 |
| D.v2=2b时,小球受到的弹力与重力大小不相等 |
如图,在倾角为α的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一只猫。已知木板的质量是猫的质量的2倍。当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变。则此时木板沿斜面下滑的加速度为( )
| A.gsinα/2 | B.gsinα | C.3gsinα/2 | D.2gsinα |
关于重力不计的带电粒子的运动的描述中,正确的是
A.只在电场( )中,带电粒子可以静止 )中,带电粒子可以静止 |
B.只在电场( )中,带电粒子可以做匀速圆周运动 )中,带电粒子可以做匀速圆周运动 |
C.只在匀强磁场( )中,带电粒子可以做匀变速曲线运动 )中,带电粒子可以做匀变速曲线运动 |
D.只在匀强磁场( )中,带电粒子一定不能做匀变速直线运动 )中,带电粒子一定不能做匀变速直线运动 |
质量为m、电荷量为q的带正电小球,从倾角为θ的粗糙绝缘斜面(µ<tanθ)上由静止下滑,斜面足够长,整个斜面置于方向水平向外的匀强磁场中,其磁感强度为B,如图所示。带电小球运动过程中,下面说法中正确的是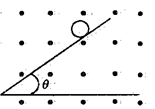
| A.小球在斜面上运动时做匀加速直线动 |
| B.小球在斜面上运动时做加速度增大,而速度也增大的变加速直线运动 |
| C.小球最终在斜面上匀速运动 |
D.小球在斜面上下滑过程中,当小球对斜面压力刚好为零时的速率为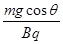 |