题目内容
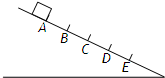 如图所示,一个小物体从光滑斜面上A点由静止开始下滑,在它通过的路程中取AE并分成相等的4段,即AB=BC=CD=DE,下列结论正确的是( )
如图所示,一个小物体从光滑斜面上A点由静止开始下滑,在它通过的路程中取AE并分成相等的4段,即AB=BC=CD=DE,下列结论正确的是( )A、物体到达各点的速率vB:vC:vD=vE=1:
| ||||||
B、物体到达各点所经历的时间tE=2tB=
| ||||||
| C、物体在BE段的平均速度等于CD段的平均速度 | ||||||
| D、物体通过每一段时,其速度增量相等 |
分析:A、根据v2=2ax,可求出物体到达各点的速度之比.
B、初速度为零的匀加速运动的推论:tB:tC:tD:tE=1:
:
:
根据这个结论判断时间关系.
C、物体做匀变速直线运动其平均速度
=
,根据速度关系判断平均速度的大小.
D、看每一段位移所用的时间是否相同去判断速度的增量关系.
B、初速度为零的匀加速运动的推论:tB:tC:tD:tE=1:
| 2 |
| 3 |
| 4 |
C、物体做匀变速直线运动其平均速度
. |
| v |
| v+v0 |
| 2 |
D、看每一段位移所用的时间是否相同去判断速度的增量关系.
解答:解:A、根据v2=2ax,v=
知物体到达各点的速度为:
vB:vC:vD:vE=1:
:
:2,故A正确;
B:因为v=at,所以有:tB:tC:tD:tE=vB:vC:vD:vE=1:
:
:2,
所以:tE=2tB=
tC=
,故B正确;
C、匀变速直线运动的平均速度
=
,又因为vB:vC:vD:vE=1:
:
:2知BE段的平均速度不等于CD段的平均速度,故C错误;
D、物体通过每一部分时间不等,所以速度的增量不等.故D错误
故选:AB.
| 2ax |
vB:vC:vD:vE=1:
| 2 |
| 3 |
B:因为v=at,所以有:tB:tC:tD:tE=vB:vC:vD:vE=1:
| 2 |
| 3 |
所以:tE=2tB=
| 2 |
| 2tD | ||
|
C、匀变速直线运动的平均速度
. |
| v |
| v+v0 |
| 2 |
| 2 |
| 3 |
D、物体通过每一部分时间不等,所以速度的增量不等.故D错误
故选:AB.
点评:解决本题的关键掌握速度位移公式v2-v02=2ax,以及平均速度的计算,初速度为0的匀加速直线运动的规律是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一个小物体由静止开始沿倾角为θ的光滑斜面下滑,m、H已知,求:
如图所示,一个小物体由静止开始沿倾角为θ的光滑斜面下滑,m、H已知,求: 如图所示,一个小物体在足够长的斜面上以一定初速度向上运动,斜面各处粗糙程度相同(μ<tanθ),初速度方向沿斜面向上,则物体在斜面上运动的过程中( )
如图所示,一个小物体在足够长的斜面上以一定初速度向上运动,斜面各处粗糙程度相同(μ<tanθ),初速度方向沿斜面向上,则物体在斜面上运动的过程中( )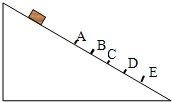 如图所示,一个小物体从光滑斜面由A点上方从静止开始下滑,在它通过的路径中取AE并分成相等的四段,vA、vB、vC、vD、vE表示通过A、B、C、D、E点的瞬时速度,v表示AE段的平均速度,则下列关系中正确的是( )
如图所示,一个小物体从光滑斜面由A点上方从静止开始下滑,在它通过的路径中取AE并分成相等的四段,vA、vB、vC、vD、vE表示通过A、B、C、D、E点的瞬时速度,v表示AE段的平均速度,则下列关系中正确的是( ) 如图所示,一个小物体在光滑斜面上,由A点从静止开始沿斜面匀加速下滑,在它经过的路径上取AE段,并将AE分成相等的四段即图中AB=BC=CD=DE,用vB表示小物体通过B点时的瞬时速度,用vC表示小物体通过C点时的瞬时速度,v表示小物体在AE段运动的平均速度,则( )
如图所示,一个小物体在光滑斜面上,由A点从静止开始沿斜面匀加速下滑,在它经过的路径上取AE段,并将AE分成相等的四段即图中AB=BC=CD=DE,用vB表示小物体通过B点时的瞬时速度,用vC表示小物体通过C点时的瞬时速度,v表示小物体在AE段运动的平均速度,则( ) (2007?广东模拟)连接A、B两点的在竖直面内的弧形轨道ACB和ADB形状相同、材料相同,如图所示.一个小物体从A点以一定初速度v开始沿轨道ACB运动,到达B点的速度为v1;若以相同大小的初逮度v沿轨道ADB运动,物体到达B点的速度为v2,比较v1和v2的大小,有( )
(2007?广东模拟)连接A、B两点的在竖直面内的弧形轨道ACB和ADB形状相同、材料相同,如图所示.一个小物体从A点以一定初速度v开始沿轨道ACB运动,到达B点的速度为v1;若以相同大小的初逮度v沿轨道ADB运动,物体到达B点的速度为v2,比较v1和v2的大小,有( )