题目内容
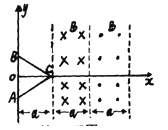
【题目】轻质弹簧原长为2l,将弹簧竖直放置在地面上,在其顶端将一质量为5m的物体由静止释放,当弹簧被压缩到最短时,弹簧长度为l.现将该弹簧水平放置,一端固定在A点,另一端与物块P接触但不连接.AB是长度为5l的水平轨道,B端与半径为l的光滑半圆轨道BCD相切,半圆的直径BD竖直,如图所示.物块P与AB间的动摩擦因数μ=0.5.用外力推动物块P,将弹簧压缩至长度l,然后释放,P开始沿轨道运动,重力加速度大小为g.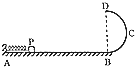
①若P的质量为m,求P到达B点时速度的大小,以及它离开圆轨道后落回到AB上的位置与B点间的距离;
②若P能滑上圆轨道,且仍能沿圆轨道滑下,求P得质量的取值范围.
【答案】解:①将弹簧竖直放置在地面上,物体下落压缩弹簧时,由系统的机械能守恒得
Ep=5mgl
如图,根据能量守恒定律得
Ep=μmg4l+ ![]()
联立解得 vB= ![]()
物体P从B到D的过程,由机械能守恒定律得
mg2l+ ![]() =
= ![]()
解得 vD= ![]()
物体P离开D点后做平抛运动,则有
2l= ![]()
x=vDt
解得 x= ![]() l
l
即落地点与B点间的距离为 ![]() .
.
②P刚好过B点,有:Ep=μm1g4l,解得 m1= ![]() m
m
P最多到C而不脱轨,则有 Ep=μm2g4l+m2gl,解得 m2= ![]() m
m
所以满足条件的P得质量的取值范围为: ![]() m≤mP<
m≤mP< ![]() m.
m.
答:①P到达B点时速度的大小是 ![]() ,它离开圆轨道后落回到AB上的位置与B点间的距离是
,它离开圆轨道后落回到AB上的位置与B点间的距离是 ![]() .②P得质量的取值范围为:
.②P得质量的取值范围为: ![]() m≤mP<
m≤mP< ![]() m.
m.
【解析】①先研究弹簧竖直的情况,根据系统的机械能守恒求出弹簧最大的弹性势能.弹簧如图放置时,由于弹簧的压缩量等于竖直放置时的压缩量,两种情况弹簧的弹性势能相等.由能量守恒定律求出物体P滑到B点时的速度,由机械能守恒定律求出物体P到达D点的速度.物体P离开D点后做平抛运动,由平抛运动的规律求水平距离.
②P能滑上圆轨道,且仍能沿圆轨道滑下,能上升的最高点为C,根据能量守恒定律列式和临界条件求解.解决本题时要抓住弹簧的形变量相等时弹性势能相等这一隐含的条件,正确分析能量是如何转化,分段运用能量守恒定律列式是关键.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案