Question

【题目】如图所示，半径为R的光滑半圆形轨道和光滑水平轨道相切，三个小球1、2、3沿水平轨道分别以速度v1＝2、v2＝3、v3＝4水平向左冲上半圆形轨道，g为重力加速度，下列关于三个小球的落点到半圆形轨道最低点A的水平距离和离开轨道后的运动形式的说法正确的是()

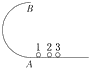
A. 三个小球离开轨道后均做平抛运动

B. 小球2和小球3的落点到A点的距离之比为∶2

C. 小球1和小球2做平抛运动的时间之比为1∶1

D. 小球2和小球3做平抛运动的时间之比为1∶1

Answer 1

【答案】BD

【解析】

先求出小球通过最高点时的临界速度，再分析三个小球能否到达最高点。若能通过最高点就能做平抛运动，再由平抛运动的规律分析水平距离和时间之比。

设小球恰好通过最高点时的速度为v，由重力提供向心力，解得： ，设小球能通过最高点时在轨道最低点时最小速度为v′，由动能定理得： ，解得：。由于v1 ，所以小球1不能到达轨道最高点，也就不能做平抛运动，故A错误；小球2和小球3离开轨道后做平抛运动，由，解得：，所以小球2和小球3做平抛运动的时间之比为1：1，故D正确；小球1做的不是平抛运动，则小球1和小球2做平抛运动的时间之比不是1：1，故C错误；设小球2和小球3通过最高点时的速度分别为v2′和v3′，根据动能定理得：

；，解得：，，由平抛运动规律得：水平距离为 x=v0t，因为时间相等，则小球2和小球3的落点到A点的距离之比为，故B正确。所以BD正确，AC错误。