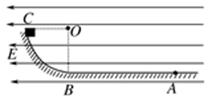
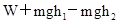题目内容
如图所示,竖直平面内的3/4圆弧形光滑轨道,轨道半径为R,A端与圆心等高,AD为水平面,B点在圆心的正下方,一小球m自A点正上方由静止释放,自由下落至A点进入轨道,小球巧好能够通过最高点C,求:
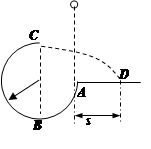
(1)小球到B点时的速度vB;
(2)释放点距A的竖直高度h;
(3)落点D与A的水平距离s。
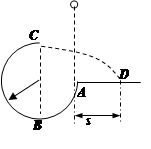
(1)小球到B点时的速度vB;
(2)释放点距A的竖直高度h;
(3)落点D与A的水平距离s。
(1) 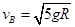 (2)
(2)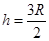 (3)
(3)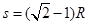
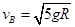 (2)
(2)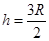 (3)
(3)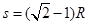
试题分析:(1)小球恰好通过最高点C点,即C点轨道弹力等于0,根据径向合力提供向心力,在最高点满足
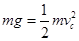 ,解得
,解得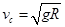 从B点到C点,光滑轨道只有重力做功,有动能定理得
从B点到C点,光滑轨道只有重力做功,有动能定理得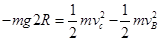 ,解得
,解得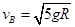
(2)从释放点到B点,只有重力做功,由动能定理得
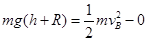 ,解得
,解得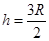
(3)物体离开轨道最高点C点后将做 平抛运动,落在AD水平面上,那么平抛的高度就是R,竖直方向自由落体运动,则有
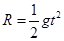 ,
,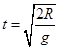 ,水平方向匀速直线运动
,水平方向匀速直线运动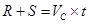 ,解得
,解得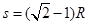

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
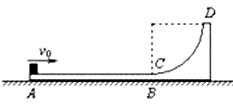
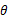 。O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件
。O、P、K三点在同一竖直平面内且O、K相距也为L,重力加速度为g,静电力常量为k,最大静摩擦力等于滑动摩擦力,小滑块初速度满足条件 。
。
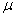 。
。