Question

【题目】某行星绕太阳沿椭圆轨道运行，如图所示，在这颗行星的轨道上有a、b、c、d四个对称点，若行星运动周期为T，则该行星（ ）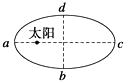

A.从a到b的运动时间等于从c到d的运动时间
B.从d经a到b的运动时间等于从b经c到d的运动时间
C.a到b的时间tab<
D.c到d的时间tcd>

Answer 1

【答案】C,D
【解析】根据开普勒第二定律知行星在近日点速度最大，远日点速度最小。行星由a到b运动时的平均速度大于由c到d运动时的平均速度，而弧长ab等于弧长cd，故A不符合题意；同理可知B不符合题意；在整个椭圆轨道上tab＝tad< ，tcd＝tcb> ，故C、D符合题意。
故答案为：C、D。此题考查对开普勒第二定律的理解和运用，由开普勒第二定律可知，远日点速度小于近日点速度，由此进行判断得出结论。