题目内容
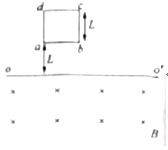
【题目】如图，两条间距L=0.5m且足够长的平行光滑金属直导轨，与水平地面成
30°角固定放置，磁感应强度B=0.4T的匀强磁场方向垂直导轨所在的斜面向上，质量
、
的金属棒ab、cd垂直导轨放在导轨上，两金属棒的总电阻r=0.2Ω，导轨电阻不计。ab在沿导轨所在斜面向上的外力F作用下，沿该斜面以
的恒定速度向上运动。某时刻释放cd， cd向下运动，经过一段时间其速度达到最大。已知重力加速度g=10m/s2，求在cd速度最大时，
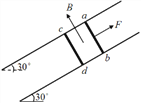
(1)abcd回路的电流强度I以及F的大小；
(2)abcd回路磁通量的变化率以及cd的速率。
【答案】(1) I=5A ,F=1.5N (2)
,
【解析】（1）以cd为研究对象，当cd速度达到最大值时，有：
①
代入数据，得： I=5A
由于两棒均沿斜面方向做匀速运动，可将两棒看作整体，作用在ab上的外力：
②
（或对ab：
）
代入数据，得： F=1.5N
（2） 设cd达到最大速度时abcd回路产生的感应电动势为E，根据法拉第电磁感应定律，有： 
③
由闭合电路欧姆定律，有：
④
联立③④并代入数据，得：
=1.0Wb/s
设cd的最大速度为vm，cd达到最大速度后的一小段时间
内，
abcd回路磁通量的变化量：
⑤
回路磁通量的变化率： 
⑥
联立⑤⑥并代入数据，得：
m/s
练习册系列答案
百年学典课时学练测系列答案
相关题目
