题目内容
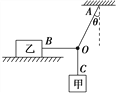
【题目】有一个推矿泉水瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败。其简化模型如下图所示,AC是长度为L1=5 m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域。已知BC长度L2=1 m,瓶子质量m=0.5 kg,瓶子与桌面间的动摩擦因数μ=0.4。某选手作用在瓶子上的水平推力F=20 N,瓶子沿AC做直线运动,假设瓶子可视为质点,g取10 m/s2,那么该选手要想游戏获得成功,试问:
(1)推力作用在瓶子上的时间最长不得超过多少?
(2)推力作用在瓶子上的距离最小为多少?

【答案】(1) ![]() (2)
(2)![]()
【解析】试题分析:(1)受力分析后,先根据牛顿第二定律求解出瓶子加速和减速时的加速度,然后根据运动学公式结合几何关系列式求解出瓶子恰好滑动到C点时推力的作用时间;
(2)瓶子恰好滑动到B点,推力的作用距离最短;根据运动学公式结合几何关系列式求解即可.
解:(1)要想游戏获得成功,瓶滑到C点速度正好为零时,推力作用时间最长,设最长作用时间为t1,有推力作用时瓶做匀加速运动,设加速度为a1,t1时刻瓶的速度为v,推力停止作用后瓶做匀减速运动,设此时加速度大小为a2,
由牛顿第二定律得:F﹣μmg=ma1,μmg=ma2
加速运动过程中的位移x1=![]()
减速运动过程中的位移x2=![]()
位移关系满足:x1+x2=L1,又:v=a1t1
由以上各式解得:t1=![]() s
s
(2)要想游戏获得成功,瓶滑到B点速度正好为零时,推力作用距离最小,设最小距离为d,则:![]() +
+![]() =L1﹣L2
=L1﹣L2
v′2=2a1d,联立解得:d="0.4" m.
答:(1)推力作用在瓶子上的时间最长不得超过![]()
(2)推力作用在瓶子上的距离最小为0.4m