Question

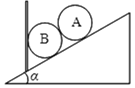
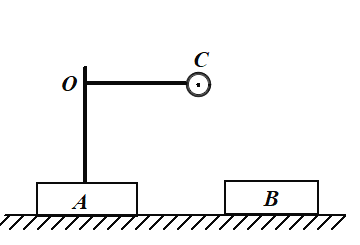
【题目】如图所示，质量均为m的木块A、B，静止于光滑水平面上。A上固定一竖直轻杆，轻杆上端的O点系一长为L的细线，细线另一端系一质量也为m的球C，现将球C拉起使细线水平伸直，并由静止释放。当球C第一次到达最低点时，木块A与B发生弹性碰撞。求：

(1)球C静止释放时A、B木块间的距离；

(2)球C向左运动的最大高度；

(3)当球C第二次经过最低点时，木块A的速度。

Answer 1

【答案】(1)(2)(3)，方向水平向左

【解析】

(1)若C到最低点过程中，A、C的水平位移为xA、xC，A、C水平动量守恒，有：

mxC=mxA

xA+xC=L

联立可解得

xA=

即球C静止释放时A、B木块间的距离为

(2)若C到最低点过程中，A、C的速度大小为vA、vC，对A、C水平动量守恒和机械能守恒，有：

mvC=mvA

解得

vA=vC=

因为A和B质量相等，弹性碰撞过程二者交换速度，则碰撞后

，vB=

当C第一次向左运动到最高点时，设A和C的共同速度为vAC，对A、C有：

联立可解得

h=

(3)C第一次到最低点至第二次到最低点的过程中，对A、C，由水平动量守恒和机械能守恒，因为A和C质量相等，二者交换速度，则木块A的速度为

方向水平向左