题目内容
【题目】如图所示，系统由左右两个侧壁绝热、底部、截面均为S的容器组成．左容器足够高，上端敞开，右容器上端由导热材料封闭．两个容器的下端由可忽略容积的细管连通．容器内两个绝热的活塞A、B下方封有氮气，B上方封有氢气．大气的压强p0 ， 温度为T0=273K，两个活塞因自身重量对下方气体产生的附加压强均为0.1p0 ． 系统平衡时，各气体柱的高度如图所示．现将系统的底部浸入恒温热水槽中，再次平衡时A上升了一定的高度．用外力将A缓慢推回第一次平衡时的位置并固定，第三次达到平衡后，氢气柱高度为0.8h．氮气和氢气均可视为理想气体．求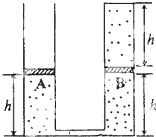
（1）第二次平衡时氮气的体积；
（2）水的温度．
【答案】
（1）解：以氢气为研究对象，初态压强为p0，体积为hS，末态体积为0.8hS．
气体发生等温变化，由玻意耳定律得：p0V1=p2V2，即：p0hS=p×0.8hS，解得：p=1.25p0①
活塞A从最高点被推回第一次平衡时位置的过程是等温过程．
该过程的初态压强为1.1p0，体积为V；末态的压强为p′，体积为V′，
则p′=p+0.1p0=1.35p0②V′=2.2hS ③
由玻意耳定律得：1.1p0×V=1.35p0×2.2hS，解得：V=2.7hS ④
答：第二次平衡时氮气的体积为2.7hS；
（2）解：活塞A从最初位置升到最高点的过程为等压过程．该过程的初态体积和温度分别为2hS和T0=273K，
末态体积为2.7hS．设末态温度为T，由盖﹣吕萨克定律得： 
= 
，解得：T=368.55K；
答：水的温度为368.55K．
【解析】（1）以B上方的氢气为研究对象，由玻意耳定律求出气体压强，然后以A下方的氮气为研究对象，由波意耳定律求出氮气的体积．（2）结合第一问的结果，求出氮气的末状态的压强，分析氮气的初末两个状态的状态参量，利用理想气体的状态方程，可求出氮气末状态的温度，即为水的温度．
