题目内容
1.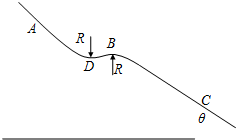 如图是一高山滑雪运动场中的滑道,BD附近是很小的一段曲道,可认为是半径均为R=40m的两圆滑连接的圆形滑道,B点和D点是两圆弧的最高点和最低点,圆弧长度远小于斜面AD及BC长度,从A到D点不考虑摩擦力的作用.一个质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,从B点水平抛出时刚好对B点没有压力,已知AB两点间的高度差为h=25m,滑道的倾角θ=37°,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
如图是一高山滑雪运动场中的滑道,BD附近是很小的一段曲道,可认为是半径均为R=40m的两圆滑连接的圆形滑道,B点和D点是两圆弧的最高点和最低点,圆弧长度远小于斜面AD及BC长度,从A到D点不考虑摩擦力的作用.一个质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,从B点水平抛出时刚好对B点没有压力,已知AB两点间的高度差为h=25m,滑道的倾角θ=37°,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:(1)运动员在B点时的速度.
(2)运动员在BC斜面的落点C到B点的距离(B点可认为是斜面上的最高点).
(3)若BD之间的高度差可忽略不计,求运动员在D点对轨道的压力.
分析 (1)从B点水平抛出时刚好对B点没有压力,可知B点靠重力提供向心力,结合牛顿第二定律求出B点的速度.
(2)根据平抛运动水平位移和竖直位移的关系求出运动的时间,结合水平位移和几何关系求出BC间的距离.
(3)根据牛顿第二定律和速度位移公式求出D点的速度,结合牛顿第二定律求出在D点所受的支持力,从而得出压力的大小.
解答 解:(1)运动员在B点时只受重力,根据牛顿第二定律有:$mg=m\frac{v_B^2}{R}$,
代入数据解得:vB=20m/s
(2)设运动员从B运动到C点的时间为t,根据平抛运动规律有:
运动员竖直位移为:y=$\frac{g{t}^{2}}{2}$ ①
运动员水平位移为:x=vBt ②
由几何关系可知:tanθ=$\frac{y}{x}$ ③
解①②③式得:t=3s
把t的值代入②式得:x=60m
所以BC的距离为:s=$\frac{x}{cosθ}$=$\frac{60}{0.8}$m=75m
(3)运动员从A运动到D的过程中,根据牛顿第二定律有:mgsinθ=ma
根据运动学规律有:${v}_{D}^{2}=2a\frac{h}{sinθ}$
运动员在D点时,根据牛顿第二定律有:FN-mg=m$\frac{{v}_{D}^{2}}{R}$
联立以上三式,代入数据解得:FN=1350N.
根据牛顿第三定律,所以运动员对D点的压力为1350N.
答:(1)运动员在B点时的速度为20m/s;
(2)运动员在BC斜面的落点C到B点的距离为75m;
(3)运动员在D点对轨道的压力为1350N.
点评 本题考查了圆周运动和平抛运动的综合运用,知道圆周运动向心力的来源,以及平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键.

练习册系列答案
相关题目
11.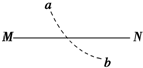 如图所示,直线MN是某电场中的一条电场线(方向未画出),虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,下列判断正确的是( )
如图所示,直线MN是某电场中的一条电场线(方向未画出),虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,下列判断正确的是( )
 如图所示,直线MN是某电场中的一条电场线(方向未画出),虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,下列判断正确的是( )
如图所示,直线MN是某电场中的一条电场线(方向未画出),虚线是一带电的粒子只在电场力的作用下,由a到b的运动轨迹,下列判断正确的是( )| A. | 电场线MN的方向一定是由N指向M | |
| B. | 带电粒子由a运动到b的过程中电势能一定逐渐减小 | |
| C. | 带电粒子在a点的速度一定小于b点的速度 | |
| D. | 带电粒子在a点的加速度一定大于在b点的加速度 |
9.关于磁感应强度B,下列说法中正确的是( )
| A. | 根据磁感应强度定义B=$\frac{F}{IL}$,磁场中某点的磁感应强度B与F成正比,与I成反比 | |
| B. | 磁感应强度B是标量,没有方向,有磁感线的地方才有磁场 | |
| C. | 在确定的磁场中,同一点的磁感应强度B是确定的,不同点的磁感应强度B可能不同,磁感线密集的地方弱感应强度B大些,磁感线稀疏的地方磁感应强度B小些 | |
| D. | 磁感应强度B是矢量,方向与F的方向相反,且唯一确定 |
6.第29届奥运会已于2008年8月在北京举行,跳水比赛是我国的传统优势项目.某运动员进行10m跳台比赛时,下列说法正确的是(不计空气阻力)( )
| A. | 为了研究运动员的技术动作,可将正在比赛的运动员视为质点 | |
| B. | 运动员在下落过程中,感觉水面在加速上升 | |
| C. | 从最高点落到水面的过程中前一半位移用的时间短,后一半位移用的时间长 | |
| D. | 从最高点落到水面的过程中前一半时间内位移大,后一半时间内位移小 |
13. 物体A放在三角形物体B的斜面上,受一平行斜面向上的拉力F作用,物体A、B都保持静止,如图所示,则( )
物体A放在三角形物体B的斜面上,受一平行斜面向上的拉力F作用,物体A、B都保持静止,如图所示,则( )
 物体A放在三角形物体B的斜面上,受一平行斜面向上的拉力F作用,物体A、B都保持静止,如图所示,则( )
物体A放在三角形物体B的斜面上,受一平行斜面向上的拉力F作用,物体A、B都保持静止,如图所示,则( )| A. | 物体A所受的摩擦力一定沿斜面向上 | |
| B. | 物体A所受的摩擦力一定沿斜面向下 | |
| C. | 地面对物体B的摩擦力一定向左 | |
| D. | 地面对物体B的摩擦力可能为零 |
10.如图给出了在平直公路上行驶的甲乙两车的速度--时间图象,设两车在开始时处于同一位置,则( )


| A. | 前5s乙的平均速度大于甲的 | B. | 在5s末两车相距最近 | ||
| C. | 在5s末两车相距最远 | D. | 在10s末两车相遇 |
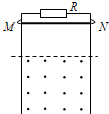 如图所示,两根竖直放置的足够长的光滑平行金属导轨间距l=0.50m,导轨上端接有电阻R=0.80Ω,导轨电阻忽略不计.导轨下部的匀强磁场区有虚线所示的水平上边界,磁感应强度B=0.40T,方向垂直于金属导轨平面向外.质量m=0.05kg,电阻r=0.20Ω的金属杆MN,从静止开始沿着金属导轨下落,下落一定高度后以v=2.5m/s的速度进入匀强磁场中,金属杆下落过程中始终与导轨垂直且接触良好.已知重力加速度g=10m/s2,不计空气阻力.
如图所示,两根竖直放置的足够长的光滑平行金属导轨间距l=0.50m,导轨上端接有电阻R=0.80Ω,导轨电阻忽略不计.导轨下部的匀强磁场区有虚线所示的水平上边界,磁感应强度B=0.40T,方向垂直于金属导轨平面向外.质量m=0.05kg,电阻r=0.20Ω的金属杆MN,从静止开始沿着金属导轨下落,下落一定高度后以v=2.5m/s的速度进入匀强磁场中,金属杆下落过程中始终与导轨垂直且接触良好.已知重力加速度g=10m/s2,不计空气阻力. 如图所示,水平轨道BC与弧形轨道AB和半圆形轨道CD平滑相接,AB、BC和CD处于同一竖直平面内,CD的半径为R.质量为m的小物块从A点由静止开始下滑,A、B间的竖直高度差为h=2.5R,不计一切摩擦,求:
如图所示,水平轨道BC与弧形轨道AB和半圆形轨道CD平滑相接,AB、BC和CD处于同一竖直平面内,CD的半径为R.质量为m的小物块从A点由静止开始下滑,A、B间的竖直高度差为h=2.5R,不计一切摩擦,求: 如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成60°角的绝缘直杆AC,其下端(C端)距地面高度h=3.2m.有一质量500克的带电小环套在直杆上,正以某一速度,沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g取l0m/s2)求:
如图所示,在水平方向的匀强电场中有一表面光滑、与水平面成60°角的绝缘直杆AC,其下端(C端)距地面高度h=3.2m.有一质量500克的带电小环套在直杆上,正以某一速度,沿杆匀速下滑,小环离杆后正好通过C端的正下方P点处.(g取l0m/s2)求: