题目内容
16. 如图所示,水平轨道BC与弧形轨道AB和半圆形轨道CD平滑相接,AB、BC和CD处于同一竖直平面内,CD的半径为R.质量为m的小物块从A点由静止开始下滑,A、B间的竖直高度差为h=2.5R,不计一切摩擦,求:
如图所示,水平轨道BC与弧形轨道AB和半圆形轨道CD平滑相接,AB、BC和CD处于同一竖直平面内,CD的半径为R.质量为m的小物块从A点由静止开始下滑,A、B间的竖直高度差为h=2.5R,不计一切摩擦,求:(1)小物块通过B点时的速度vB的大小;
(2)小物块通过半圆形轨道最低点C时,轨道对物块的支持力F的大小.
分析 (1)A到B过程由机械能守恒定律即可求得物体通过B点时的速度;
(2)物体做圆周运动,则由牛顿第二定律可求得支持力F的大小.
解答 解:(1)物块从A点运动到B点的过程中,由机械能守恒得:
mgh=$\frac{1}{2}$m${v}_{B}^{2}$
解得:vB=$\sqrt{2gh}$=$\sqrt{5gR}$.
(2)物块从B至C做匀速直线运动,有:vC=vB=$\sqrt{5gR}$.
物块通过圆形轨道最低点C时,做圆周运动,由牛顿第二定律有:
F-mg=m$\frac{{v}_{C}^{2}}{R}$
可得:F=6mg.
答:(1)小物块通过B点时的速度vB的大小是$\sqrt{5gR}$;
(2)小物块通过半圆形轨道最低点C时,轨道对物块的支持力F的大小是6mg.
点评 本题考查动能定理及竖直面内的圆周运动,选择合适的过程,并注意竖直面内圆周运动的临界条件即可求解.

练习册系列答案
相关题目
7.物体做匀变速直线运动,某时刻速度的大小为6m/s,1s后速度的大小变为10m/s,关于该物体在这1s内的位移和加速度大小,下列说法正确的是( )
①位移的大小可能小于6m
②位移的大小可能大于10m
③加速度的大小可能小于4m/s2
④加速度的大小可能大于10m/s2.
①位移的大小可能小于6m
②位移的大小可能大于10m
③加速度的大小可能小于4m/s2
④加速度的大小可能大于10m/s2.
| A. | ②④ | B. | ①④ | C. | ②③ | D. | ①③ |
2.下列关于动量守恒的论述正确的是( )
| A. | 某物体沿着光滑斜面下滑,物体的动量守恒 | |
| B. | 系统在某方向上所受的合外力为零,则系统在该方向上动量守恒 | |
| C. | 如果系统内部有相互作用的摩擦力,系统的机械能必然减少,系统的动量也不再守恒 | |
| D. | 系统虽然受到几个较大的外力,但合外力为零,系统的动量仍然守恒 |
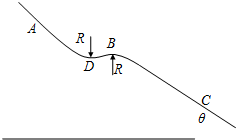 如图是一高山滑雪运动场中的滑道,BD附近是很小的一段曲道,可认为是半径均为R=40m的两圆滑连接的圆形滑道,B点和D点是两圆弧的最高点和最低点,圆弧长度远小于斜面AD及BC长度,从A到D点不考虑摩擦力的作用.一个质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,从B点水平抛出时刚好对B点没有压力,已知AB两点间的高度差为h=25m,滑道的倾角θ=37°,sin37°=0.6,cos37°=0.8,取g=10m/s2.求:
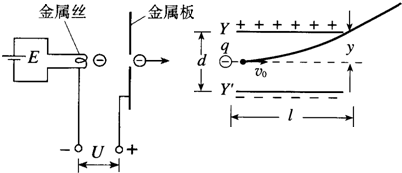
如图是一高山滑雪运动场中的滑道,BD附近是很小的一段曲道,可认为是半径均为R=40m的两圆滑连接的圆形滑道,B点和D点是两圆弧的最高点和最低点,圆弧长度远小于斜面AD及BC长度,从A到D点不考虑摩擦力的作用.一个质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,从B点水平抛出时刚好对B点没有压力,已知AB两点间的高度差为h=25m,滑道的倾角θ=37°,sin37°=0.6,cos37°=0.8,取g=10m/s2.求: 为测量一阻值约为21Ω的电阻,可供选择的器材如下:
为测量一阻值约为21Ω的电阻,可供选择的器材如下: