题目内容
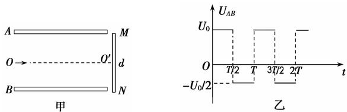
 如图甲所示,水平放置的平行金属板A和B间的距离为d,金属板长L=2
如图甲所示,水平放置的平行金属板A和B间的距离为d,金属板长L=2| 3 |
(1)若在A、B板间加一恒定电压U=U0,则要使粒子穿过金属板后恰好打到小孔K,求U0的大小;
(2)若在A、B板间加上如图乙所示的电压,电压为正表示A板比B板的电势高,其中T=
| 2L |
| v0 |
| T |
| 2 |
分析:利用类平抛运动的知识求电压;粒子在水平方向做匀速直线运动,粒子运动的时间都为
,再根据类平抛运动求解时间.
| T |
| 2 |
解答:解:(1)粒子做类平抛运动,则:
水平方向:L=V0t
竖直方向:
=
×
t2
又L=2
d
联立得:U0=
(2)粒子在水平方向做匀速直线运动,粒子运动的时间都为:
t=
=
设粒子在t′时刻进入金属板,粒子类平抛运动的时间为t″,则;
=
×
t″2
又L=2
d
联立得:t″=
所以t′=t-t″=
答:(1)要使粒子穿过金属板后恰好打到小孔K,U0=
;
(2)能打到小孔K的粒子在
时从O点射入.
水平方向:L=V0t
竖直方向:
| d |
| 2 |
| 1 |
| 2 |
| qU0 |
| md |
又L=2
| 3 |
联立得:U0=
| ||
| 12q |
(2)粒子在水平方向做匀速直线运动,粒子运动的时间都为:
t=
| L |
| V0 |
| T |
| 2 |
设粒子在t′时刻进入金属板,粒子类平抛运动的时间为t″,则;
| d |
| 2 |
| 1 |
| 2 |
| q.4U0 |
| md |
又L=2
| 3 |
联立得:t″=
| T |
| 4 |
所以t′=t-t″=
| T |
| 4 |
答:(1)要使粒子穿过金属板后恰好打到小孔K,U0=
| ||
| 12q |
(2)能打到小孔K的粒子在
| T |
| 4 |
点评:要做好本题需要理解粒子的运动过程,利用类平抛运动的知识是比较方便的方法.

练习册系列答案
相关题目
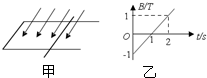 如图甲所示,水平放置的U形金属导轨宽度为25cm,其电阻不计.阻值为2?的金属棒与导轨垂直放置.金属棒与导轨左端相距40cm.匀强磁场与水平面的夹角为30°斜向下,从t=0时刻起磁感应强度随时间的变化如图乙所示.已知在0~2s内金属棒始终处于静止状态.则下列说法中正确的是( )
如图甲所示,水平放置的U形金属导轨宽度为25cm,其电阻不计.阻值为2?的金属棒与导轨垂直放置.金属棒与导轨左端相距40cm.匀强磁场与水平面的夹角为30°斜向下,从t=0时刻起磁感应强度随时间的变化如图乙所示.已知在0~2s内金属棒始终处于静止状态.则下列说法中正确的是( )| A、在t=0时,金属棒所受安培力为零 | B、在t=1s时,金属棒所受安培力为零 | C、在t=0与t=2s时,金属棒所受安培力大小相等 | D、在t=0到t=2s时间内流过金属棒横截面积的电荷量为0.05C |

 如图甲所示,水平放置的平行金属导轨连接一个平行板电容器C和电阻R,导体棒MN放在导轨上且接触良好,整个装置放于垂直导轨平面的磁场中,磁感应强度B的变化情况如图乙所示(图示磁感应强度方向为正),MN始终保持静止,则0~t2时间( )
如图甲所示,水平放置的平行金属导轨连接一个平行板电容器C和电阻R,导体棒MN放在导轨上且接触良好,整个装置放于垂直导轨平面的磁场中,磁感应强度B的变化情况如图乙所示(图示磁感应强度方向为正),MN始终保持静止,则0~t2时间( )