题目内容
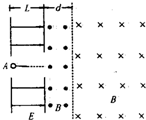如图所示，空间分布着图示的匀强电场E（宽为L）和匀强磁场B，一带电粒子质量为m，电量为q，（不计重力）从A点由静止释放后经电场加速后进入磁场，穿过中间磁场进入右边磁场后能按某一路径再返回A点而重复前述过程．求中间磁场的宽度d和粒子的运动周期（虚线为磁场分界线，并不表示有什么障碍物）分析：（1）带正电的粒子在电场中做匀加速直线运动，垂直进入磁场后做匀速圆周运动，画出粒子运动的轨迹，根据动能定理即可求解带电粒子在磁场中运动的速率；
粒子在磁场中由洛伦兹力充当向心力，由牛顿第二定律求出轨迹的半径．根据几何关系求解中间磁场区域的宽度；
（2）先求出在电场中运动的时间，再求出在两段磁场中运动的时间，三者之和即带电粒子运动的周期．
粒子在磁场中由洛伦兹力充当向心力，由牛顿第二定律求出轨迹的半径．根据几何关系求解中间磁场区域的宽度；
（2）先求出在电场中运动的时间，再求出在两段磁场中运动的时间，三者之和即带电粒子运动的周期．
解答：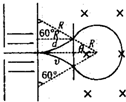
解：（1）由题意，粒子在磁场中的轨迹应关于υ方向的直线对称，如图所示，
电场中：qEL=
mv2 ①
v=at1=
t1 ②
由几何知识：sinθ=
=
所以θ=30°
又qvB=
③
d=Rsin60° ④
联立以上公式可得：d=
（2）粒子在磁场中的周期：T=
=
在中间磁场的时间：t2=2×
=
⑤
在右边磁场的时间：t3=
?T=
⑥
由①③④得 T′=2t1+t2+t3=2
+
答：中间磁场的宽度d=
，粒子的运动周期T′=2
+
．
解：（1）由题意，粒子在磁场中的轨迹应关于υ方向的直线对称，如图所示，电场中：qEL=
| 1 |
| 2 |
v=at1=
| qE |
| m |
由几何知识：sinθ=
| R |
| 2R |
| 1 |
| 2 |
又qvB=
| mv2 |
| R |
d=Rsin60° ④
联立以上公式可得：d=
| ||
| 2qB |
（2）粒子在磁场中的周期：T=
| 2πR |
| v |
| 2πm |
| qB |
在中间磁场的时间：t2=2×
| T |
| 6 |
| 2πm |
| 3qB |
在右边磁场的时间：t3=
| 300° |
| 360° |
| 5πm |
| 3qB |
由①③④得 T′=2t1+t2+t3=2
|
| 7πm |
| 3qB |
答：中间磁场的宽度d=
| ||
| 2qB |
|
| 7πm |
| 3qB |
点评：本题是带电粒子在组合场中运动的问题，解题关键是画出粒子的运动轨迹，运用几何知识求解轨迹半径．
练习册系列答案
相关题目
（2012?台州二模）如图所示，空间分布着宽为L，垂直于纸面向里的匀强磁场．一金属线框从磁场左边界匀速向右通过磁场区域．规定逆时针方向为电流的正方向，则感应电流随位移变化的关系图（i-x）正确的是（ ）
（2011?东莞一模）如图所示，空间分布着方向平行于纸面且与场区边界垂直的有界匀强电场，电场强度为E、场区宽度为L．在紧靠电场右侧的圆形区域内，分布着垂直于纸面向外的匀强磁场，磁感应强度B未知，圆形磁场区域半径为r．一质量为m、电荷量为q的带正电的粒子从A点由静止释放后，在M点离开电场，并沿半径方向射入磁场区域，然后从N点射出，O为圆心，∠MON=120°，粒子重力可忽略不计．求：
25②（供选用《选修3-l》物理课教材的学生做）
如图所示，空间分布着有理想边界的匀强电场和匀强磁场，已知左侧匀强电场的场强大小为E、方向水平向右，其宽度为L；中间区域匀强磁场的磁感应强度大小为B、方向垂直纸面向外；右侧匀强磁场的磁感应强度大小也为B、方向垂直纸面向里．一个带正电的粒子（质量为m、电荷量为q，不计重力）从电场左边缘a点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到了a点，然后重复上述运动过程．求：