题目内容
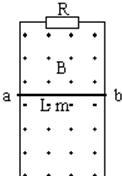 如图所示,竖直放置的U形导轨宽为L=1.5m,上端串有电阻R=15Ω,磁感应强度为B=2T的匀强磁场方向垂直纸面向外.金属棒ab质量m=0.1kg,电阻r=3Ω,与导轨接触良好,导轨电阻不计,不计摩擦,从静止释放后保持水平而下滑,g=10m/s2.
如图所示,竖直放置的U形导轨宽为L=1.5m,上端串有电阻R=15Ω,磁感应强度为B=2T的匀强磁场方向垂直纸面向外.金属棒ab质量m=0.1kg,电阻r=3Ω,与导轨接触良好,导轨电阻不计,不计摩擦,从静止释放后保持水平而下滑,g=10m/s2.(1)求其下滑的最大速度vm.
(2)求达到最大速度时金属棒两端的电势差Uab.
分析:(1)金属棒向下先做加速度逐渐减小的加速运动,当加速度减小到0,即安培力等于重力时,速度达到最大.推导出安培力与速度的关系式,再由平衡条件求解ab的最大速度vm.
(2)由公式E=BLvm求出达到最大速度时金属棒产生的感应电动势,再根据串联电路的性质求解金属棒两端的电势差Uab.
(2)由公式E=BLvm求出达到最大速度时金属棒产生的感应电动势,再根据串联电路的性质求解金属棒两端的电势差Uab.
解答:解:(1)达到最大速度vm时棒中的感应电流为:
I=
=
…①
棒所受的安培力为:F=BIL… ②
则得:F=
… ③
速度最大时棒ab做匀速运动,受力平衡,则得:
F=mg…④
由③、④得:vm=
=
m/s=2m/s
(2)棒达到最大速度时产生的感应电动势为:
E=BLvm=2×1.5×2V=6V
则ab间的电势差为:Uab=
=
V=5V
答:(1)其下滑的最大速度vm为2m/s.
(2)达到最大速度时金属棒两端的电势差Uab为5V.
I=
| E |
| R+r |
| BLvm |
| R+r |
棒所受的安培力为:F=BIL… ②
则得:F=
| B2L2vm |
| R+r |
速度最大时棒ab做匀速运动,受力平衡,则得:
F=mg…④
由③、④得:vm=
| mg(R+r) |
| B2L2 |
| 0.1×10×(15+3) |
| 22×1.52 |
(2)棒达到最大速度时产生的感应电动势为:
E=BLvm=2×1.5×2V=6V
则ab间的电势差为:Uab=
| ER |
| R+r |
| 6×15 |
| 15+3 |
答:(1)其下滑的最大速度vm为2m/s.
(2)达到最大速度时金属棒两端的电势差Uab为5V.
点评:对于导体在导轨上滑动类型,分析棒的运动情况是解题的基础,关键要会推导安培力与速度,可在理解的基础上记住结论:F=
.
| B2L2v |
| R+r |

练习册系列答案
相关题目
 如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为
如图所示,竖直放置的光滑圆环上套有一质量为m的小球,小球经过最高点时的速度为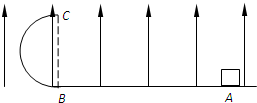 如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小
如图所示,竖直放置的半圆形绝缘轨道半径为R,下端与绝缘水平面平滑连接,整个装置处于方向竖直向上的匀强电场E中.一质量为m、带电量为+q的物块(可视为质点),从水平面上的A点以初速度v0水平向左运动,沿半圆形轨道恰好通过最高点C,场强大小 如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )
如图所示,竖直放置的轻弹簧一端固定在地面上,另一端与斜面体P固定,P与斜放的固定挡板MN接触且处于静止状态,则斜面体P此刻受到外力的个数可能是( )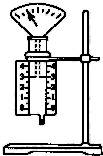 物理选修3-3
物理选修3-3 如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求
如图所示,竖直放置的U形导轨宽为L,上端串有电阻R(其余导体部分的电阻都忽略不计).磁感应强度为B的匀强磁场方向垂直于纸面向外.金属棒ab的质量为m,与导轨接触良好,不计摩擦.从静止释放后ab保持水平而下滑.试求