题目内容
【题目】如图，在竖直平面内有一个半径为R的光滑圆弧轨道，半径OA竖直、OC水平，一个质量为m的小球自C点的正上方P点由静止开始自由下落，从C点沿切线进入轨道，小球沿轨道到达最高点A时恰好对轨道没有压力。重力加速度为
，不计一切摩擦和阻力。求：
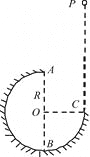
（1）小球到达轨道最高点A时的速度大小；
（2）小球到达轨道最低点B时对轨道的压力大小。
【答案】（1）
（2）
【解析】试题分析：（1） 设小球在A点速度大小为
，小球到达A点由重力提供向心力得：
①………………………………………………2分
可得： 
……………………………………………………2分
设小球在B点速度大小为
，从B到A由机械能守恒得：
②………………………………………2分
在B点由牛顿第二定律可得： 
③ ……………… 2分
由①②③计算可得： 
……………………………………………1分
在B点，小球对轨道的压力为
，由牛顿第三定律可得：
④………………………………………1分
阅读快车系列答案
【题目】某同学利用竖直上抛小球的频闪照片验证机械能守恒定律。频闪仪每隔0.05s 闪光一次，用毫米刻度尺测得相邻两个时刻小球上升的高度分别为s1=26.3cm，s2=23.68cm，s3=21.16cm，s4=18.66cm，s5=16.04cm，该同学通过计算得到不同时刻的速度如下表所示（当地重力加速度g=9.80m/s2，小球质量m=0.10kg）：
时刻 |
|
|
|
|
速度（m/s） | 4.48 | 3.98 | 3.47 |
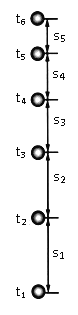
（1）上面测量高度的五个数据中不符合有效数字读数要求的是 段，应记作 cm；
（2）由频闪照片上的数据计算t2时刻小球的速度
＝__________m/s；(计算结果保留三位有效数字）
（3）从t2到t5时间内，重力势能增量
＝_________J，动能减少量
＝________J；（计算结果保留三位有效数字）
（4）在误差允许的范围内，若
与
近似相等，从而验证了机械能守恒定律。由上述计算所得_____（选填“>”、“<”或“＝”），造成这种结果的主要原因是 。
