题目内容
（2006?安徽模拟）来自质子源的质子（初速度为零），经一直线加速器加速，形成电流为I的细柱形质子流，已知质子源与靶间的距离为d，质子电荷量为e，假定分布在质子源到靶间的加速度是均匀的，质子到达靶时的速度为υ，则质子源与靶间的质子数为（ ）
分析：质子数与电荷量有关系，电荷量有与电流和质子的飞行时间有关．设飞行时间为t，通过位移与速度的关系，可求出运动的时间．然后电荷量与电流的关系，q=It，所以质子数为n=
，从而即可求解．
| q |
| e |
解答：解：距离为d，速度为v，则时间：t=
电流为I，则在t时间内通过的电量为q=It=
所以质子数目：
N=
=
故B正确．
故选：B．
| d | ||
|
电流为I，则在t时间内通过的电量为q=It=
| 2Id |
| v |
所以质子数目：
N=
| q |
| e |
| 2Id |
| ev |
故B正确．
故选：B．
点评：掌握总电量=单一粒子子带电量与总个数的积；及电流的表达式I=
的应用，同时要注意建立正确的物理模型．
| q |
| t |
练习册系列答案
相关题目
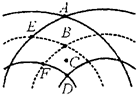（2006?安徽模拟）如图所示表示两列相干水波某时刻的波峰和波谷位置，实线表示波峰，虚线表示波谷，相邻实线与虚线间的距离为0.2m，波速为1m/s，在图示范围内可以认为这两列波的振幅均为1cm，C点是相邻实线与虚线间的中点，则（ ）
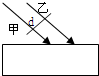（2006?安徽模拟）如图所示，两束平行的甲光和乙光，相距为d，斜射到置于空气中的平行玻璃砖上，当它们从玻璃砖的下表面射出时（ ）