题目内容
2.某同学在“用双缝干涉测光的波长”的实验中,实验装置如图1所示.使用的双缝间距为d=0.025cm.实验时,首先调节光源和滤光片的中心位于遮光筒的中心轴线上,并使单缝和双缝竖直且互相平行.当屏上出现了干涉图样后,通过测量头(与螺旋测微器原理相似,手轮转动一周,分划板前进或后退0.500mm)观察第一条亮纹的位置如图2(a)所示,第五条亮纹位置如图2(b)所示,测出双缝与屏的距离为L=50.00cm,则图2(a)读数为x1=1.128 mm,图2(b)读数为x2=5.880 mm,待测光的波长λ的公式为λ=$\frac{d({x}_{2}-{x}_{1})}{4L}$,代入测量数据可得λ=594 nm.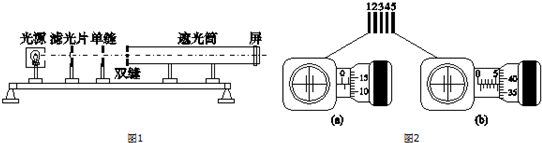
分析 固定仪器时要使单缝和双缝竖直且平行,螺旋测微器的读数等于固定刻度读数加上可动刻度读数,需估读.根据双缝干涉条纹的间距公式求出波长的表达式,从而求出波长的大小.
解答 解:实验时,首先调节光源和滤光片的中心使之位于遮光筒的中心轴线上,并使单缝和双缝竖直且平行;
乙图中,螺旋测微器的固定刻度读数为1mm,可动刻度读数为0.01×12.8mm=0.128mm,则最终读数为1.128mm.
丙图中,螺旋测微器的固定刻度读数为5.5mm,可动刻度读数为0.01×38.0mm=0.380mm,则最终读数为5.880mm.
相邻条纹间距△x=$\frac{{x}_{2}-{x}_{1}}{4}$,
根据△x=$\frac{L}{d}$λ得,λ=$\frac{△xd}{L}$=$\frac{d({x}_{2}-{x}_{1})}{4L}$.
代入数据得,λ=$\frac{(5.880-1.128)×1{0}^{-3}×0.025×1{0}^{-2}}{4×0.5}$=5.94×10-7m=594nm.
故答案为:滤光片,双缝,0.628,5.880,$\frac{d({x}_{2}-{x}_{1})}{4L}$,594.
点评 解决本题的关键掌握游标卡尺的读数方法,掌握双缝干涉条纹的间距公式,并能灵活运用,基础题.

练习册系列答案
相关题目
16. 如图,正点电荷放在O 点,图中画出它产生的电场的六条对称分布的电场线.以水平电场线上的O′点为圆心画一个圆,与电场线分别相交于 a、b、c、d、e,下列说法正确的是( )
如图,正点电荷放在O 点,图中画出它产生的电场的六条对称分布的电场线.以水平电场线上的O′点为圆心画一个圆,与电场线分别相交于 a、b、c、d、e,下列说法正确的是( )
 如图,正点电荷放在O 点,图中画出它产生的电场的六条对称分布的电场线.以水平电场线上的O′点为圆心画一个圆,与电场线分别相交于 a、b、c、d、e,下列说法正确的是( )
如图,正点电荷放在O 点,图中画出它产生的电场的六条对称分布的电场线.以水平电场线上的O′点为圆心画一个圆,与电场线分别相交于 a、b、c、d、e,下列说法正确的是( )| A. | b、e两点的电场强度相同 | |
| B. | a点电势低于e点电势 | |
| C. | b、c两点间电势差等于 e、d两点间电势差 | |
| D. | 电子沿圆周由d运动到 c,电场力做负功 |
17. 空间存在某电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点O处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )
空间存在某电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点O处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )
 空间存在某电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点O处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )
空间存在某电场,一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动.粒子质量为m,初速度大小为v0,其电势能Ep随坐标x变化的关系如图所示,图线关于纵轴左右对称,以无穷远处为零电势能点,粒子在原点O处电势能为E0,在x1处电势能为E1,则下列说法中正确的是( )| A. | 坐标原点O处两侧电场方向相反 | |
| B. | 粒子经过x1、-x1处速度相同 | |
| C. | 由x1运动到O过程电场力做正功 | |
| D. | 若粒子能够沿x轴负方向运动越过O点,一定有v0>$\sqrt{\frac{2({E}_{0}-{E}_{1})}{m}}$ |
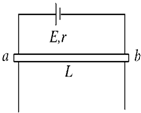 如图所示,电源电动势E=2V,r=0.5Ω,竖直光滑导轨宽L=0.2m,导轨电阻不计.另有一金属棒ab,质量m=0.1kg,电阻R=0.5Ω,金属棒靠在导轨的外面.为使金属棒静止不下滑,施加一个与纸面夹角为30°且方向向里的匀强磁场,g取10m/s2.
如图所示,电源电动势E=2V,r=0.5Ω,竖直光滑导轨宽L=0.2m,导轨电阻不计.另有一金属棒ab,质量m=0.1kg,电阻R=0.5Ω,金属棒靠在导轨的外面.为使金属棒静止不下滑,施加一个与纸面夹角为30°且方向向里的匀强磁场,g取10m/s2.
 如图所示,匀强电场方向水平向右,一带负电微粒沿笔直的虚线在电场中斜向上运动,则该微粒在从A运动到B的过程中,其动能将减小,电势能将增加(填“增大”或“减小).
如图所示,匀强电场方向水平向右,一带负电微粒沿笔直的虚线在电场中斜向上运动,则该微粒在从A运动到B的过程中,其动能将减小,电势能将增加(填“增大”或“减小).