题目内容
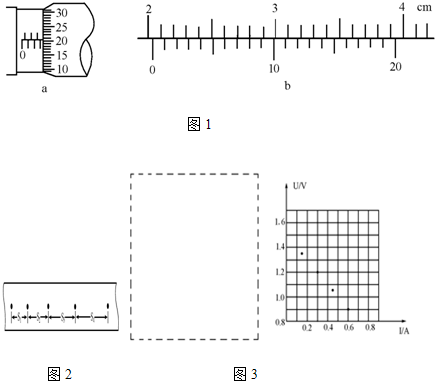
㈠(1)某学生用螺旋测微器在测定某一金属丝的直径时,测得的结果如下图1所示,则该金属丝的直径d=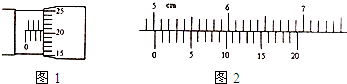
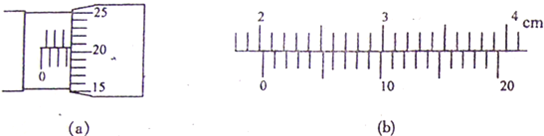
(2)如图3是某同学用打点计时器做的“研究小车的匀变速直线运动”实验时打出的一条纸带,A、B、C、D、E为该同学在纸带上选的计数点,相邻计数点间还有4个点未画出.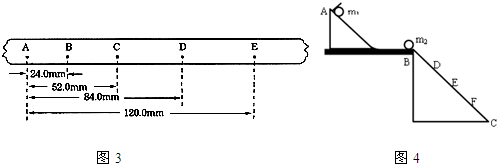
由图3可知:打点计时器打下D点时小车的瞬时速度为
㈡、为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同,质量不等的小球,按下述步骤做了如下实验:
①用天平测出两小球的质量分别为m1 和m2,且 m1>m2
②按照如图4所示的那样,安装好实验装置.将斜槽AB固定在桌边,使槽的末端点的切线水平.并与斜面BC连接在斜槽末端.
③先不放小球m2,让小球m1 从斜槽顶端A处由静止开始滚下,记下小球在斜面上的落点位置.
④将小球m2 放在斜槽前端边缘处,让小球m1从斜槽顶端A处滚下,使它们发生碰撞.记下小球m1和小球m2在斜面上的落点置.
⑤用毫米刻度尺量出各落点位置到斜槽末端点B的距离.图4中D、E、F点是该同学记下的小球在斜面上的几个落点位置,到B点的距离分别为LD,LE,LF.
根据该同学的实验,回答下列问题:
(1)小球m1与m2发生碰撞后,m1的落点是图中的点
(2)用测得的物理量来表示,只要满足关系式
(3)用测得的物理量来表示,只要再满足关系式
3.206
3.206
mm.另一位学生用游标尺上标有20等分刻度的游标卡尺测一工件的长度,测得的结果如图所2示,则该工件的长度L=5.015
5.015
cm.
(2)如图3是某同学用打点计时器做的“研究小车的匀变速直线运动”实验时打出的一条纸带,A、B、C、D、E为该同学在纸带上选的计数点,相邻计数点间还有4个点未画出.

由图3可知:打点计时器打下D点时小车的瞬时速度为
0.34
0.34
m/s,小车的加速度为0.4
0.4
m/s2㈡、为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失),某同学选取了两个体积相同,质量不等的小球,按下述步骤做了如下实验:
①用天平测出两小球的质量分别为m1 和m2,且 m1>m2
②按照如图4所示的那样,安装好实验装置.将斜槽AB固定在桌边,使槽的末端点的切线水平.并与斜面BC连接在斜槽末端.
③先不放小球m2,让小球m1 从斜槽顶端A处由静止开始滚下,记下小球在斜面上的落点位置.
④将小球m2 放在斜槽前端边缘处,让小球m1从斜槽顶端A处滚下,使它们发生碰撞.记下小球m1和小球m2在斜面上的落点置.
⑤用毫米刻度尺量出各落点位置到斜槽末端点B的距离.图4中D、E、F点是该同学记下的小球在斜面上的几个落点位置,到B点的距离分别为LD,LE,LF.
根据该同学的实验,回答下列问题:
(1)小球m1与m2发生碰撞后,m1的落点是图中的点
D
D
,m2的落点是图中的点F
F
.(2)用测得的物理量来表示,只要满足关系式
m1
=m1
+m2
| LE |
| LD |
| LF |
m1
=m1
+m2
,则说明碰撞中动量是守恒的.| LE |
| LD |
| LF |
(3)用测得的物理量来表示,只要再满足关系式
m1LE=m1LD+m2LF
m1LE=m1LD+m2LF
,则说明两小球的碰撞时弹性碰撞.分析:(一)(1)螺旋测微器固定刻度与可动刻度的示数之和是螺旋测微器的读数;游标卡尺主尺示数与游标尺示数之和是游标尺的示数.
(2)做匀变速运动的物体在某段时间内的平均速度等于这都时间中间时刻的瞬时速度,据此求出D点的瞬时速度;做匀变速直线运动的物体在相邻的相等时间内的位移之差等于at2,据此求出物体的加速度.
(二)(1)m1与m2相撞后,m2的速度增大,m1的速度减小,m1的速度小于m2的速度,它们都做平抛运动,m1的水平位移小于m2的水平位移,据此确定两球的落点;
(2)如果两球碰前的总动量等于碰后的总动量,则碰撞过程中动量守恒.
(3)如果碰前的总动能等于碰后总动能,则两小球的碰撞是弹性碰撞.
(2)做匀变速运动的物体在某段时间内的平均速度等于这都时间中间时刻的瞬时速度,据此求出D点的瞬时速度;做匀变速直线运动的物体在相邻的相等时间内的位移之差等于at2,据此求出物体的加速度.
(二)(1)m1与m2相撞后,m2的速度增大,m1的速度减小,m1的速度小于m2的速度,它们都做平抛运动,m1的水平位移小于m2的水平位移,据此确定两球的落点;
(2)如果两球碰前的总动量等于碰后的总动量,则碰撞过程中动量守恒.
(3)如果碰前的总动能等于碰后总动能,则两小球的碰撞是弹性碰撞.
解答:解:(一)(1)由图1所示螺旋测微器可知,螺旋测微器的固定刻度示数是3mm,
可动刻度示数是20.6×0.01mm=0.206mm,螺旋测微器的示数是3mm+0.206mm=3.206mm;
由图2所示游标卡尺可知,主尺示数是5cm,游标尺示数是3×0.05mm=0.15mm=0.015cm,
则游标卡尺的示数是5cm+0.015cm=5.015cm.
(2)由图3可知:sCE=sAE-sAC=120.0mm-52.0mm=68mm=0.068m,
则在D点时小车的瞬时速度vD=
=
=0.34m/s;
由图3可知:sDE=sAE-sAD=120.0mm-84.0mm=36mm=0.036m,
sCD=sAD-sAC=84.0mm-52.0mm=32.0mm=0.032m,
小车的加速度a=
=
=0.4m/s2;
(二)(1)m1与m2相撞后,m2的速度增大,m1的速度减小,m1的速度小于m2的速度,它们都做平抛运动,
m1的水平位移小于m2的水平位移,因此E点是碰前m1的落地点,D是碰后m1的落地点,F是碰后m2的落地点.
(2)设斜面BC的倾角是θ,小球离开斜槽AB后做平抛运动;
碰前小球m1的落地点是E,它的水平位移x1=LEcosθ=v1t1,
竖直位移y1=LEsinθ=
gt12,解得v1=LEcosθ
;
碰后小球m1的落地点是D,它的水平位移x1′=LDcosθ=v1′t1′,
竖直位移y1′=LD′sinθ=
gt12,解得v1′=LDcosθ
;
碰后小球m2的落地点是F,它的水平位移x2=LFcosθ=v2t2,
竖直位移y2′=LFsinθ=
gt2′2,解得v2′=LFcosθ
;
如果m1v1=m1v1′+m2v2′,m1LEcosθ
=m1LDcosθ
+m2LFcosθ
,
即当m1
=m1
+m2
时,说明碰撞中动量是守恒的.
如果
m1v12=
m1v1′2+
m2v2′2,即当m1LE=m1LD+m2LF时,说明两小球的碰撞时弹性碰撞.
故答案为:(一)(1)3.206;5.015;(2)0.34;0.4;
(二)(1)D;F;(2)m1
=m1
+m2
;(3)m1LE=m1LD+m2LF.
可动刻度示数是20.6×0.01mm=0.206mm,螺旋测微器的示数是3mm+0.206mm=3.206mm;
由图2所示游标卡尺可知,主尺示数是5cm,游标尺示数是3×0.05mm=0.15mm=0.015cm,
则游标卡尺的示数是5cm+0.015cm=5.015cm.
(2)由图3可知:sCE=sAE-sAC=120.0mm-52.0mm=68mm=0.068m,
则在D点时小车的瞬时速度vD=
| sCE |
| tCE |
| 0.068m |
| 0.1s×2 |
由图3可知:sDE=sAE-sAD=120.0mm-84.0mm=36mm=0.036m,
sCD=sAD-sAC=84.0mm-52.0mm=32.0mm=0.032m,
小车的加速度a=
| sDE-sCD |
| t2 |
| 0.036m-0.032m |
| (0.1s)2 |
(二)(1)m1与m2相撞后,m2的速度增大,m1的速度减小,m1的速度小于m2的速度,它们都做平抛运动,
m1的水平位移小于m2的水平位移,因此E点是碰前m1的落地点,D是碰后m1的落地点,F是碰后m2的落地点.
(2)设斜面BC的倾角是θ,小球离开斜槽AB后做平抛运动;
碰前小球m1的落地点是E,它的水平位移x1=LEcosθ=v1t1,
竖直位移y1=LEsinθ=
| 1 |
| 2 |
|
碰后小球m1的落地点是D,它的水平位移x1′=LDcosθ=v1′t1′,
竖直位移y1′=LD′sinθ=
| 1 |
| 2 |
|
碰后小球m2的落地点是F,它的水平位移x2=LFcosθ=v2t2,
竖直位移y2′=LFsinθ=
| 1 |
| 2 |
|
如果m1v1=m1v1′+m2v2′,m1LEcosθ
|
|
|
即当m1
| LE |
| LD |
| LF |
如果
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(一)(1)3.206;5.015;(2)0.34;0.4;
(二)(1)D;F;(2)m1
| LE |
| LD |
| LF |
点评:(一)本题考查了螺旋测微器与游标卡尺的读数问题,要注意:螺旋测微器需要估读,而游标卡尺不需要估读.
熟练应用匀变速直线运动的运动规律即可求出瞬时速度与加速度.
(二)验证动量守恒定律时,物体的速度不易测量,常用物体的位移来间接测出速度,这是解题的关键.
熟练应用匀变速直线运动的运动规律即可求出瞬时速度与加速度.
(二)验证动量守恒定律时,物体的速度不易测量,常用物体的位移来间接测出速度,这是解题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目