Question

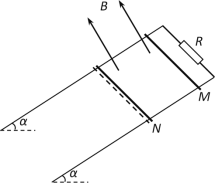
【题目】如图所示，两根电阻不计且足够长的平行金属导轨倾斜放置，倾角α=37°，导轨间距L=1m，顶端用电阻R=2Ω的定值电阻相连。虚线上方存在垂直于导轨所在平面向上的匀强磁场，磁感应强度大小B=1T。质量m1=0.1kg、电阻R1=4Ω的导体棒M在磁场中距虚线的距离d=2m，M与导轨间的动摩擦因数μ1=0.25，质量m2=0.3kg、电阻R2=2Ω的导体棒N在虚线处，N与导轨间的动摩擦因数μ2=0.8。将导体棒M、N同时从导轨上由静止释放，M到达虚线前已经匀速，重力加速度g取10m/s2，运动过程中M、N与导轨始终接触良好，已知sin37°=0.6，cos37°=0.8。

（1）求M、N相碰前，M上产生的焦耳热；

（2）求M、N相碰前M运动的时间；

（3）M、N相遇发生弹性碰撞，碰后瞬间对M施加一个沿斜面方向的作用力F，使M、N同时匀减速到零，求M棒在减速到零的过程中作用力F的大小随时间变化的表达式。

Answer 1

【答案】（1）0.48J；（2）1.5s；（3）F=0.96－0.08t(t≤2.5s)

【解析】

（1）M棒匀速时，有

m1gsin37°=μ1m1gcos37°＋BIL①

E=BLv0②

③

④

M棒从开始到达虚线位置，有

⑤

M棒、N棒、电阻R产生的焦耳热之比为

QM∶QN∶QR=8∶1∶1⑥

QM=⑦

由①~⑦式解得

QM=0.48J

（2）对M棒由动量定理有

(m1gsin37－μ1m1gcos37°－BL)t=m1v0⑧

q=t=⑨

Φ=BLd⑩

t=1.5s

（3）对M、N棒碰撞过程，有

m1v0=m1v1＋m2v2

碰后对N棒

μ2m2gcos37°－m2gsin37=m2a2

v2=a2t0

碰后对M棒

m1gsin37＋μ1m1gcos37°＋BI′L－F=m1a1

v1=a1t0

t0=2.5s

由～式解得

F=0.96－0.08t(t≤2.5s)