题目内容
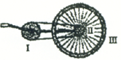 如图是自行车传动机构的示意图,其中I是大齿轮,II是小齿轮,IlI是后车轮.假设踏板的转速为nr/s.
如图是自行车传动机构的示意图,其中I是大齿轮,II是小齿轮,IlI是后车轮.假设踏板的转速为nr/s.(1)则大齿轮的角速度是
2πn
2πn
rad/s.(2)已知大齿轮Ⅰ的半径r1,小齿轮II的半径为r2,自行车车轮的半径为R,则自行车前进速度的表达式:
| 2πnRr1 |
| r2 |
| 2πnRr1 |
| r2 |
分析:(1)根据脚踏板的转速知道其频率,从而求出脚踏板的角速度,抓住脚踏板和大此轮的角速度相等求出大齿轮的角速度.
(2)通过大小齿轮的线速度相等求出小齿轮的角速度,根据小齿轮的角速度与后轮的速度相等求出自行车的线速度,从而确定要测量的物理量.
(2)通过大小齿轮的线速度相等求出小齿轮的角速度,根据小齿轮的角速度与后轮的速度相等求出自行车的线速度,从而确定要测量的物理量.
解答:解:(1)脚踏板的角速度ω=2πn.则大齿轮的角速度为2πn.
(2)设后轮的半径为R,因为大小齿轮的线速度相等,ω1r1=ω2r2,所以ω2=
,小齿轮和后轮的角速度相等,则线速度v=Rω2=
.
故答案为:(1)2πn
(2)
.
(2)设后轮的半径为R,因为大小齿轮的线速度相等,ω1r1=ω2r2,所以ω2=
| ω1r1 |
| r2 |
| 2πnRr1 |
| r2 |
故答案为:(1)2πn
(2)
| 2πnRr1 |
| r2 |
点评:解决本题的关键知道靠链条传动,线速度相等,共轴转动,角速度相等.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 (2006?扬州二模)如图是自行车传动机构的示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.
(2006?扬州二模)如图是自行车传动机构的示意图,其中Ⅰ是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.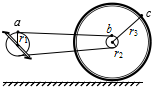 如图是自行车传动机构的示意图,a、b、c分别是大齿轮、小齿轮和后轮边缘上的点.已知大齿轮、小齿轮和后轮的半径分别为r1、r2和r3,若a点的线速度大小为v,则b点的线速度大小为
如图是自行车传动机构的示意图,a、b、c分别是大齿轮、小齿轮和后轮边缘上的点.已知大齿轮、小齿轮和后轮的半径分别为r1、r2和r3,若a点的线速度大小为v,则b点的线速度大小为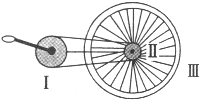 如图是自行车传动机构的示意图,其中I是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.已知大齿轮转速为n r/s;
如图是自行车传动机构的示意图,其中I是大齿轮,Ⅱ是小齿轮,Ⅲ是后轮.已知大齿轮转速为n r/s;