Question

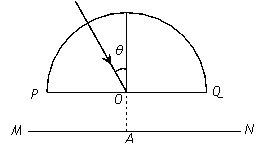
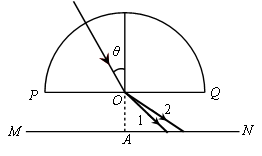
如图所示为一半圆形玻璃砖，光屏MN与直径PQ平行，圆心O到MN的距离为d，一由两种单色光组成的复色光与竖直方向成θ=30^°角射入玻璃砖的圆心，在光屏上出现了两个光斑，玻璃对两种单色光的折射率分别为n₁=和n₂=，求：

①离A点最远的光斑与A点之间的距离x；

②为使光屏上的光斑消失，复色光的入射角至少为多少？

 

Answer 1

【答案】

①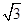d，②C=45°

【解析】

试题分析：经分析可知2光折射后光斑离A点远

①由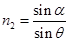   （1分）  

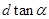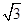x==d   （1分）

②由题意分析可知，当1光光斑消失后，2光光斑也消失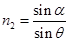，的最小值为1光的临界角

由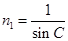   （1分）   

得C=45°   （1分）

考点：光的折射