Question

（2013?威海模拟）如图所示为一半圆形玻璃砖，光屏MN与直径PQ平行，圆心O到MN的距离为d，一由两种单色光组成的复色光与竖直方向成θ=30°角射入玻璃砖的圆心，在光屏上出现了两个光斑，玻璃对两种单色光的折射率分别为n₁=

2

和n₂=

3

，求：
①离A点最远的光斑与A点之间的距离x；
②为使光屏上的光斑消失，复色光的入射角至少为多少？

Answer 1

分析：①根据折射定律n=

sini

sinr

分析可知，光从光密介质射入光疏介质时，折射率越大，折射角越大，偏折程度越大，可确定出2光折射后光斑离A点远．根据折射定律求出折射角，由几何关系求解x．
②当1光光斑消失后，2光光斑也消失，θ的最小值为1光的临界角，根据临界角公式sinC=

1

n

求解．

解答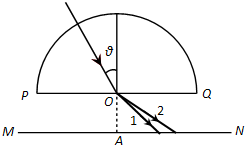：解：由题意：玻璃对两种单色光的折射率分别为n₁=

2

和n₂=

3

，根据折射定律n=

sini

sinr

分析可知，光从光密介质射入光疏介质时，折射率越大，折射角越大，偏折程度越大，经分析可知2光折射后光斑离A点远．
①设光线2的折射角为α．
由n2=

sinα

sinθ

得：sinα=n₂sinθ=

3

?sin30°=

3

2

，
得：α=60°．
由几何关系得：x=dtanα=

3

d．
②由题意分析可知，当1光光斑消失后，2光光斑也消失，θ的最小值为1光的临界角
由n1=

1

sinC

=

1

2

     得：C=45°
答：
①离A点最远的光斑与A点之间的距离x是

3

d．
②为使光屏上的光斑消失，复色光的入射角至少为45°．

点评：本题根据折射率的大小，应正确判断出偏折程度的大小．对于涉及全反射的问题，要紧扣全反射产生的条件：一是光从光密介质射入光疏介质；二是入射角大于临界角，并要掌握临界角公式sinC=

1

n

．