题目内容
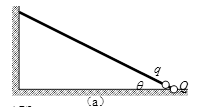
如图所示,光滑水平桌面上有一质量为m的物块,桌面右下方有半径为R的光滑圆弧形轨道,圆弧所对应的圆心角为2θ,轨道左右两端点A、B等高,左端A与桌面的右端的高度差为H.已知物块在一向右的水平拉力作用下沿桌面由静止滑动,撤去拉力后物块离开桌面,落到轨道左端时其速度方向与轨道相切,随后沿轨道滑动,若轨道始终与地面保持静止(重力加速度为g).
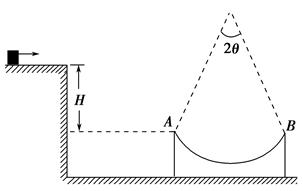
求:(1)拉力对物块做的功;
(2)物块滑到轨道最低点时受到的支持力大小.

求:(1)拉力对物块做的功;
(2)物块滑到轨道最低点时受到的支持力大小.
(1)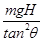 (2)(3-2cos θ)mg+
(2)(3-2cos θ)mg+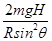
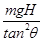 (2)(3-2cos θ)mg+
(2)(3-2cos θ)mg+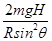
(1)A点的速度vA分解如图,则v0=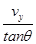 ①
①
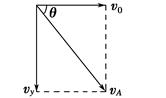
竖直方向v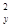 =2gH②
=2gH②
由动能定理WF=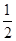 mv
mv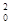 ③
③
联立①②③式解得WF=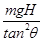 ④
④
(2)在A点,vA=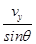 ⑤
⑤
从A到最低点由机械能守恒定律得
mgR(1-cos θ)=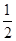 mv2-
mv2-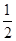 mv
mv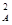 ⑥
⑥
在最低点对物块由牛顿第二定律得
FN-mg=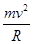 ⑦
⑦
联立②⑤⑥⑦式解得
FN=(3-2cos θ)mg+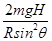 ⑧
⑧
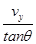 ①
①
竖直方向v
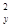 =2gH②
=2gH②由动能定理WF=
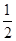 mv
mv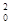 ③
③联立①②③式解得WF=
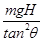 ④
④(2)在A点,vA=
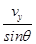 ⑤
⑤从A到最低点由机械能守恒定律得
mgR(1-cos θ)=
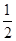 mv2-
mv2-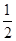 mv
mv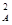 ⑥
⑥在最低点对物块由牛顿第二定律得
FN-mg=
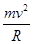 ⑦
⑦联立②⑤⑥⑦式解得
FN=(3-2cos θ)mg+
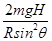 ⑧
⑧
练习册系列答案
相关题目
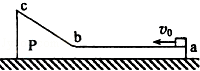

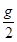 的加速度竖直下落h的过程中,下列说法中正确的是( )
的加速度竖直下落h的过程中,下列说法中正确的是( )