题目内容
 [物理一选修3-5]
[物理一选修3-5](1)如图1所示为氢原子的能级示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外发出光子,用这些光照射逸出功为2.49eV的金属钠,下列说法正确的是
A.这群氢原子能发出三种频率不同的光,其中从n=3跃迁到n=2所发出的光波长最短
B.这群氢原子能发出两种频率不同的光,其中从n=3跃迁到n=1所发出的光频率最高
C.金属钠表面所发出的光电子的初动能最大值为11.11eV
D.金属钠表面所发出的光电子的初动能最大值为9.60eV
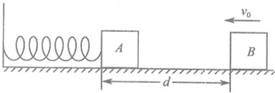
(2)在光滑的水平面上,质量为m1的小球A以速率V0向右运动.在小球A的前方O点处有一质量为m2的小球B处于静止状态,如图2所示.小球A与小球B发生正碰后小球A与小球B均向右运动.小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO.假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性碰撞,求A、B两小球的质量之比.
分析:(1)根据玻尔理论分析氢原子发出的三种频率不同的光的波长、频率关系.从n=3跃迁到n=1所发出的光能量最大,产生金属钠表面所发出的光电子的初动能最大,根据爱因斯坦光电效应方程求出初动能的最大值.
(2)根据碰后再次相遇的路程关系,求出小球碰后的速度大小之比,根据碰撞过程中动量、能量守恒列方程即可求出两球的质量之比.
(2)根据碰后再次相遇的路程关系,求出小球碰后的速度大小之比,根据碰撞过程中动量、能量守恒列方程即可求出两球的质量之比.
解答:解:(1)A、B这群氢原子能发出三种频率不同的光,根据玻尔理论△E=Em-En(m>n)得知,从n=3跃迁到n=1所发出的光能量最大,由E=hγ=h
得知,频率最高,波长最短.故AB错误.
C、D从n=3跃迁到n=1所发出的光能量最大,光照射逸出功为2.49eV的金属钠,所发出的光电子的初动能最大,根据爱因斯坦光电效应方程得,EK=hγ-W=(E3-E1)-W=[-1.51-(-13.6)]-2.49=9.60eV.故C错误,D正确.
故选D
(2)从两小球碰撞后到它们再次相遇,小球A和小球B的速度大小保持不变,设两小球通过的路程分别为s1、s2.
由v=
得:
=
两小球碰撞过程有:m1v0=m1v1+m2v2
m1v02=
m1v12+
m2v22
解得:
=2
答:A、B两小球的质量之比2:1.
| c |
| λ |
C、D从n=3跃迁到n=1所发出的光能量最大,光照射逸出功为2.49eV的金属钠,所发出的光电子的初动能最大,根据爱因斯坦光电效应方程得,EK=hγ-W=(E3-E1)-W=[-1.51-(-13.6)]-2.49=9.60eV.故C错误,D正确.
故选D
(2)从两小球碰撞后到它们再次相遇,小球A和小球B的速度大小保持不变,设两小球通过的路程分别为s1、s2.
由v=
| s |
| t |
| v1 |
| v2 |
| 1 |
| 4 |
两小球碰撞过程有:m1v0=m1v1+m2v2
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得:
| m1 |
| m2 |
答:A、B两小球的质量之比2:1.
点评:(1)解决本题的关键知道能级间跃迁能量与光子频率的关系,以及掌握光电效应方程.
(2)解答本题的突破口是根据碰后路程关系求出碰后的速度大小之比,本题很好的将直线运动问题与动量守恒和功能关系联系起来,比较全面的考查了基础知识.
(2)解答本题的突破口是根据碰后路程关系求出碰后的速度大小之比,本题很好的将直线运动问题与动量守恒和功能关系联系起来,比较全面的考查了基础知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
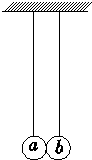 [物理一选修3-5]如图,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触.现摆球a向左拉开一小角度后释放.若两球的碰撞是弹性的,下列判断正确的是( )
[物理一选修3-5]如图,大小相同的摆球a和b的质量分别为m和3m,摆长相同,并排悬挂,平衡时两球刚好接触.现摆球a向左拉开一小角度后释放.若两球的碰撞是弹性的,下列判断正确的是( )| A、第一次碰撞后的瞬间,两球的速度大小相等 | B、第一次碰撞后的瞬间,两球的动量大小相等 | C、第一次碰撞后,两球的最大摆角不相同 | D、发生第二次碰撞时,两球在各自的平衡位置的右侧 |
 [物理--一选修3-5]
[物理--一选修3-5]