题目内容
【题目】如图所示，在xOy平面内，以O′(0，R)为圆心，R为半径的圆内有垂直平面向外的匀强磁场，x轴下方有垂直平面向里的匀强磁场，两区域磁感应强度大小相等．第四象限有一与x轴成45°角倾斜放置的挡板PQ，P，Q两点在坐标轴上，且O，P两点间的距离大于2R，在圆形磁场的左侧0<y<2R的区间内，均匀分布着质量为m，电荷量为＋q的一簇带电粒子，当所有粒子均沿x轴正向以速度v射入圆形磁场区域时，粒子偏转后都从O点进入x轴下方磁场，结果有一半粒子能打在挡板上．不计粒子重力，不考虑粒子间相互作用力．求：
(1)磁场的磁感应强度B的大小；
(2)挡板端点P的坐标；
(3)挡板上被粒子打中的区域长度．
【答案】(1)
（2）P点的坐标为
（3）
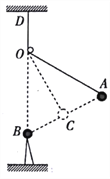
【解析】试题分析：（1）（8分）设一粒子自磁场边界A点进入磁场，该粒子由O点射出圆形磁场，轨迹如图甲所示，过A点做速度的垂线长度为r,C为该轨迹圆的圆心.连接AOˊ、CO，可证得ACOOˊ为菱形，根据图中几何关系可知：粒子在圆形磁场中的轨道半径r=R，（3分）
由
（3分）
得：（2分）
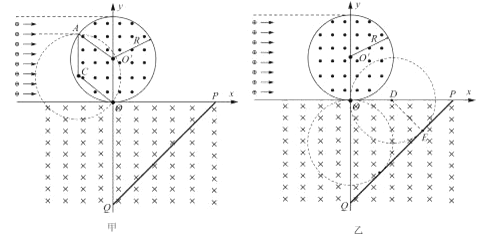
（2）（4分）有一半粒子打到挡板上需满足从O点射出的沿x轴负方向的粒子、沿y轴负方向的粒子轨迹刚好与挡板相切，如图乙所示，过圆心D做挡板的垂线交于E点，（1分）
（2分）
P点的坐标为（
，0 ） （1分）
（3）（7分）设打到挡板最左侧的粒子打在挡板上的F点，如图丙所示，OF=2R ① （1分）
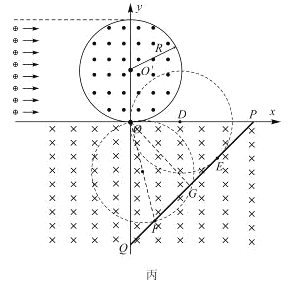
过O点做挡板的垂线交于G点，
② （2分）
③ （2分）
④ （1分）
挡板上被粒子打中的区域长度l=FE=
+
=
⑤ （1分）
（说明：如果用余弦定理求解，也给相应分，将②③ 的4分 分为公式和结果各给2分）
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
