题目内容
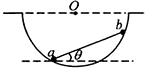 两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,如图所示。已知小球a和b的质量之比为
两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,如图所示。已知小球a和b的质量之比为![]() ,细杆长度、是球面半径的
,细杆长度、是球面半径的![]() 倍。两球处于平衡状态时,细杆与水平面的夹角θ是
倍。两球处于平衡状态时,细杆与水平面的夹角θ是
A.45° B.30° C.22.5° D.15°
D
解析:
由题目中的数据可以得出,abO三点组成一个等腰直角三角形。所以两底角都为![]() 。对两球进行受力分析,由于球面光滑,所以两球都只受到3个力,如图所示:重力、球面的支持力、刚性细杆的弹力。由于是刚性细杆,所以刚性细杆对两球的弹力均沿着杆方向,且对两球的弹力大小相等。两球处于平衡状态是,两球受到的合力都为零。两球受到的三个力都组成一个封闭的力的矢量三角形。再由正弦定理列出等式。对球
。对两球进行受力分析,由于球面光滑,所以两球都只受到3个力,如图所示:重力、球面的支持力、刚性细杆的弹力。由于是刚性细杆,所以刚性细杆对两球的弹力均沿着杆方向,且对两球的弹力大小相等。两球处于平衡状态是,两球受到的合力都为零。两球受到的三个力都组成一个封闭的力的矢量三角形。再由正弦定理列出等式。对球![]() :
:![]() ,对球
,对球![]() :
:![]() ,所以:
,所以:![]() ,即
,即![]() ,所以
,所以![]() 。答案D正确。
。答案D正确。


练习册系列答案
相关题目
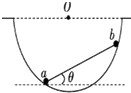 两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连放置在一个光滑的半球面内,如图所示,已知细杆长度是球面的半径的
两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连放置在一个光滑的半球面内,如图所示,已知细杆长度是球面的半径的 如图所示,两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,已知小球a和b的质量分别为
如图所示,两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,已知小球a和b的质量分别为 两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,如图所示.已知小球a和b的质量之比为
两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,如图所示.已知小球a和b的质量之比为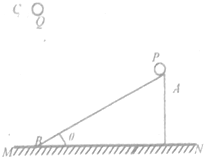 (2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数
(2013?湖北模拟)如图所示,有一倾角为θ=37°的斜面AB固定在水平面MN上.现有两个可视为质点的小球P和Q,同时由静止开始释放,小球P从斜面最高点A点沿斜面运动到斜面最低点B点,小球P与斜面间的摩擦因数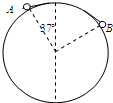 一光滑圆柱体,固定在地面上,现用长为圆柱体的
一光滑圆柱体,固定在地面上,现用长为圆柱体的