题目内容
有一种“双聚焦分析器”质谱仪,工作原理如图所示。加速电场的电压为U,静电分析器中有辐向会聚电场,即与圆心O1等距各点的电场强度大小相同,方向沿径向指向圆心O1;磁分析器中以O2为圆心、圆心角为90°的扇形区域内,分布着方向垂直于纸面向外的匀强磁场,其左边界与静电分析器的右边界平行.由离子源发出一个质量为m、电荷量为q的正离子(初速度为零,重力不计),经加速电场加速后,从M点沿垂直于该点的电场方向进入静电分析器,在静电分析器中,离子沿半径为R的四分之一圆弧轨道做匀速圆周运动,并从N点射出静电分析器.而后离子由P点沿着既垂直于磁分析器的左边界,又垂直于磁场方向射入磁分析器中,最后离子沿垂直于磁分析器下边界的方向从Q点射出,并进入收集器.测量出Q点与圆心O2的距离为d,位于Q点正下方的收集器入口离Q点的距离为d/2.(题中的U、m、q、R、d都为已知量)
(1)求静电分析器中离子运动轨迹处电场强度E的大小;
(2)求磁分析器中磁感应强度B的大小;
(3)现将离子换成质量为4m ,电荷量仍为q的另一种正离子,其它条件不变.磁分析器空间足够大,离子不会从圆弧边界射出,收集器的位置可以沿水平方向左右移动,要使此时射出磁分析器的离子仍能进入收集器,求收集器水平移动的距离.
(1) ; (2)
; (2) ;(3)
;(3)
解析试题分析:(1)离子经电场直线加速,由动能定理: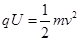
离子在静电分析器中做匀速圆周运动,根据牛顿第二定律,有:
联立解得:
(2)离子在磁分析器中做匀速圆周运动,根据牛顿第二定律,有:
由题意可知,圆周运动的轨道半径:
解得:
(3)另一正离子经电场加速后的速度
可得磁场中运动的半径为
水平向右移动的距离为

考点:本题考查了带点离子在组合场中的运动、圆周运动、直线加速。

一圆环形铝质金属圈(阻值不随温度变化)放在匀强磁场中,设第1s内磁感线垂直于金属圈平面(即垂直于纸面)向里,如图甲所示。若磁感应强度B随时间t变化的关系如图乙所示,那么第3s内金属圈中 ( )
| A.感应电流逐渐增大,沿逆时针方向 |
| B.感应电流恒定,沿顺时针方向 |
| C.圆环各微小段受力大小不变,方向沿半径指向圆心 |
| D.圆环各微小段受力逐渐增大,方向沿半径指向圆心 |
如图所示,矩形线圈abcd位于通电长直导线附近,线圈与导线在同一平面内,线圈的ad、bc边与导线平行。下面的操作不能使线圈中产生感应电流的是
| A.使线圈水平向左平移 | B.使线圈水平向右平移 |
| C.使线圈竖直向下平移 | D.使线圈以bc边为轴转动 |
如图所示,用两根足够长的粗糙金属条折成“┌”型导轨,右端水平,左端树直,与导轨等宽的粗糙金属细杆ab、cd与导轨垂直且接触良好。已知ab、cd杆的质量、电阻值均相等,导轨电阻不计,整个装置处于竖直向上的匀强磁场中。当ab杆在水平向右的拉力F作用下沿导轨向右匀速运动时,cd杆沿轨道向下运动,以下说法正确的是( )
| A.cd杆一定向下做匀加速直线运动 |
| B.拉力F的大小一定不变 |
| C.回路中的电流强度一定不变 |
| D.拉力F的功率等于ab棒上的焦耳热功率与摩擦热功率之和 |




 的正电荷置于电场中O点由静止释放,经过
的正电荷置于电场中O点由静止释放,经过 后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求:
后,电荷以v0=1.5×104m/s的速度通过MN进入其右方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻,忽略磁场变化带来的影响)。求:
 时刻电荷与O点的竖直距离r。
时刻电荷与O点的竖直距离r。