��Ŀ����
10�� ����m=10kg�������ڷ���ƽ����б�桢��СΪF=186N�����������£��ӹ̶��ֲ�б��ĵ��ɾ�ֹ��ʼ��б�������˶�������F����t1=2s��ȥ����֪б����ˮƽ��ļнǦ�=37�㣬��ͼ��ʾ��б���㹻����������б���Ķ�Ħ��������=0.8��ȡ�������ٶ�g=10m/s2����
����m=10kg�������ڷ���ƽ����б�桢��СΪF=186N�����������£��ӹ̶��ֲ�б��ĵ��ɾ�ֹ��ʼ��б�������˶�������F����t1=2s��ȥ����֪б����ˮƽ��ļнǦ�=37�㣬��ͼ��ʾ��б���㹻����������б���Ķ�Ħ��������=0.8��ȡ�������ٶ�g=10m/s2������1��������F�����£�����ļ��ٶȴ�Сa1
��2����ȥ����F��������б�����ϻ��е�ʱ��t2
��3�����ж������ܷ�ص�б��ˣ���������˵�����ɣ���������������ӳ������ص�б��˵�ʱ�䣨sin37��=0.6��cos37��=0.8��
���� ��1������ţ�ٵڶ������������ʱ����ļ��ٶȣ�
��2��ͨ���˶�ѧ��ʽ�����ȥ����ʱ���ٶȣ�����ţ�ٵڶ����������ȥ������ļ��ٶȣ��Ӷ������ٶ�ʱ�乫ʽ�����б���ϻ���ʱ�䣮
��3�������������»����������Ħ�����Ĺ�ϵ�����������ܷ��»��������»�������ţ�ٵڶ����ɺ�λ��ʱ�乫ʽ���ʱ�䣮
��� �⣺��1����������F����������ļ��ٶȴ�СΪa1������ţ�ٵڶ����� ��
F-��mgsin��+��mgcos�ȣ�=ma1
��� a1=$\frac{F}{m}$-g��sin��+��cos�ȣ�=$\frac{186}{10}$-10����0.6+0.8��0.8��=6.2m/s2��
��2����2sĩ���ٶ�Ϊv1�����˶���ʽ ��v1=a1t1=6.2��2=12.4m/s
��ȥF��������б���������ȼ���ֱ���˶�������ٶȴ�СΪa2���˶����ٶ�Ϊ�����õ�ʱ��Ϊt2������ţ�ٵڶ����ɡ��˶�ѧ��ʽ��
mgsin��+��mgcos��=ma2
��ã�a2=12.4m/s2
��0=v1+��-a2��t2
��� t2=$\frac{{v}_{1}}{{a}_{2}}$=$\frac{12.4}{12.4}$s=1s
��3������ߵ�ʱ������mgsin37�㣼��mgcos37�㣬�������岻���»�����ֹ��б���ϣ�
��
��1��������F�����£�����ļ��ٶȴ�Сa1��6.2m/s2��
��2����ȥ����F��������б�����ϻ��е�ʱ��t2��1s��
��3�������岻�ܻص�б��ˣ�
���� �����ۺϿ�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ��֪�����ٶ�����ϵ��ѧ���˶�ѧ���������Ƕ���ѧ�����б��������

| A�� | �������뷴������ͬʱ������ͬʱ��ʧ | |
| B�� | �������뷴�����������Dz�ͬ���ʵ��� | |
| C�� | �����������ķ��������ĺ���Ϊ�� | |
| D�� | ֻ�е������崦�ھ�ֹʱ������֮����������뷴��������С����� |
| A�� | ƽ���˶����ٶȡ����ɵȶ������뻯ģ�� | |
| B�� | ����ѧ���������������Dz��ñ�ֵ������� | |
| C�� | ������������������Χ���ڵ糡�Ĺ۵� | |
| D�� | ��ɵ���Χ���е糡Ҳ�дų�����ӳ�˵�ʹ����ܲ��ɷֵ� |
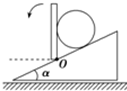 ��ͼ��ʾ��һС����б���ϴ��ھ�ֹ״̬��������һ��Ħ�����������ֱ��������ֱλ�û�����O��ת��ˮƽλ�ã���˹��������б���ѹ��F1����Ե����ѹ��F2�ı仯����ǣ�������
��ͼ��ʾ��һС����б���ϴ��ھ�ֹ״̬��������һ��Ħ�����������ֱ��������ֱλ�û�����O��ת��ˮƽλ�ã���˹��������б���ѹ��F1����Ե����ѹ��F2�ı仯����ǣ�������| A�� | F1һֱ��С��F2�ȼ�С������ | B�� | F1�ȼ�С������F2��������С | ||
| C�� | F1��F2��һֱ��С | D�� | F1��F2��һֱ���� |
| A�� | $\frac{{\sqrt{2}}}{2}T$ | B�� | $\frac{3}{4}T$ | C�� | $\frac{{\sqrt{3}}}{2}T$ | D�� | $\frac{1}{2}T$ |
| A�� | $\sqrt{\frac{2}{5}}$s | B�� | ����$\sqrt{\frac{2}{5}}$s | C�� | ��$\sqrt{\frac{2}{5}}$s | D�� | $\frac{\sqrt{2}}{5}$s |
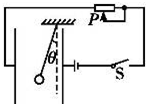 һ����С��������ƽ�а�������ڲ����պϿ���S��������������������ֱ����н�Ϊ�ȣ���ͼ��ʾ�����з�������ʹ�нǦȼ�С���ǣ�������
һ����С��������ƽ�а�������ڲ����պϿ���S��������������������ֱ����н�Ϊ�ȣ���ͼ��ʾ�����з�������ʹ�нǦȼ�С���ǣ�������| A�� | ���ֿ��رպϣ�ʹ�����忿��һЩ | |
| B�� | ���ֿ��رպϣ�ʹ������������Ƭ�����ƶ� | |
| C�� | ���ֿ��رպϣ�ʹ������Զ��һЩ | |
| D�� | �Ͽ����أ�ʹ�����忿��һЩ |
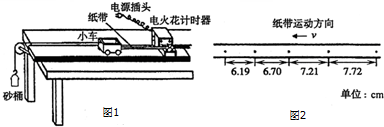
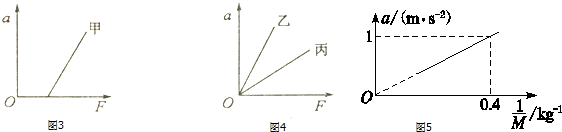
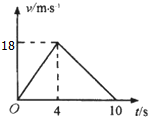 ����Ϊ4kg�����壬��0��4s����ˮƽ��F��Ħ����f�����ã���4��10s������Ħ����f�����ö�ֹͣ����v-tͼ����ͼ��ʾ����
����Ϊ4kg�����壬��0��4s����ˮƽ��F��Ħ����f�����ã���4��10s������Ħ����f�����ö�ֹͣ����v-tͼ����ͼ��ʾ����