题目内容
若已知行星绕太阳公转的半径为r,公转的周期为T,万有引力恒量为G,则由此可求出( )
| A.某行星的质量 | B.太阳的质量 |
| C.某行星的密度 | D.太阳的密度 |
B
解析试题分析:行星绕太阳做匀速圆周运动,根据万有引力提供向心力,列出等式只能求出中心体的质量,故A错误; 行星绕太阳公转可认为做匀速圆周运动,根据万有引力提供向心力,列出等式: ,解得:
,解得: ,故B正确; 不清楚行星的质量和体积,所以不能求出行星的密度,故C错误; 不知道太阳的体积,所以不能求出太阳的密度,故D错误;因此选B.
,故B正确; 不清楚行星的质量和体积,所以不能求出行星的密度,故C错误; 不知道太阳的体积,所以不能求出太阳的密度,故D错误;因此选B.
考点:本题考查圆周运动和万有引力定律及其应用,意在考查学生运用万有引力定律解快问题的能力.

来自中国航天科技集团公司的消息称,中国自主研发的北斗二号卫星系统今年起进入组 网高峰期,预计在2015年形成覆盖全球的卫星导航定位系统,此系统由中轨道、高轨道和同步轨道卫星等组成.现在正在服役的北斗一号卫星定位系统的三颗卫星都定位在距地面36000km的地球同步轨道上.目前我国的各种导航定位设备都要靠美国的GPS系统提供服务,而美国的全球卫星定位系统GPS由24颗卫星组成,这些卫星距地面的高度均为20000km.则下列说法中正确的是
| A.所有GPS的卫星所受向心力大小均相等 |
| B.所有GPS的卫星比北斗一号的卫星线速度大 |
| C.北斗二号中的中轨道卫星的加速度一定大于高轨道卫星的加速度 |
| D.北斗一号系统中的三颗卫星向心加速度比赤道上物体的向心加速度小 |
经国际小行星命名委员会命名的“神舟星”和“杨利伟星”的轨道均处在火星和木星轨道之间,它们绕太阳沿椭圆轨道运行,其轨道参数如下表。
| | 远日点 | 近日点 |
| 神舟星 | 3.575AU | 2.794AU |
| 杨利伟星 | 2.197AU | 1.649AU |
“神舟星”和“杨利伟星”绕太阳运行的周期分别为T1和T2,它们在近日点的加速度分别为a1和a2。则下列说法正确的是
A.
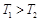 ,
,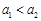 B.
B.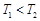 ,
,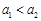
C.
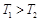 ,
,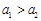 D.
D.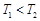 ,
,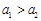
“天宫一号”目标飞行器在距地面约350km的圆轨道上运行,则飞行器
| A.速度大于7.9km/s |
| B.加速度小于9.8m/s2 |
| C.运行周期为24h |
| D.角速度小于地球自转的角速度 |
质量为m的探月航天器在接近月球表面的轨道上飞行,其运动视为匀速圆周运动。已知月球质量为M,月球半径为R,月球表面重力加速度为g,引力常量为G,不考虑月球自转的影响,则航天器的
A.线速度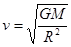 |
B.角速度为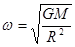 |
C.运行周期为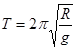 |
D.向心加速度为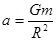 |
2012年6月18日,“神舟九号”飞船经5次变轨追“天宫一号”.如果将“神舟九号”飞船的五次变轨简化为如图所示的二次变轨:由轨道Ⅰ变至轨道Ⅱ,再变至轨道Ⅲ.下列关于“神舟九号”飞船的描述正确的是
| A.沿轨道Ⅱ从P向Q的运动过程中机械能增加 |
| B.沿轨道Ⅱ从P向Q的运动过程中速度逐渐变小 |
| C.沿轨道Ⅲ运动的机械能比沿轨道Ⅰ运动的机械能大 |
| D.沿轨道Ⅲ运动的加速度比沿轨道Ⅰ运动的加速度小 |
设地球表面的重力加速度为g0,物体在距离地面为3R(R是地球半径)空中,由于地球的作用产生的加速度为g,则g/g0为
| A.1/3 | B.1/9 | C.1/4 | D.1/16 |
两个质点之间万有引力的大小为F,如果将这两个质点之间的距离变为原来的2倍,那么它们之间万有引力的大小变为
| A.F/4 | B.4F | C.16F | D.F/16 |
假设我国发射的探月卫星“嫦娥一号”的绕月运行轨道和载人飞船“神舟七号”的绕地运行轨道都可以看成是圆轨道,且不计卫星到月球表面的距离和飞船到地球表面的距离.已知月球质量约为地球质量的1/81,月球半径约为地球半径的1/4,地球上的第一宇宙速度约为7.9 km/s,卫星和飞船的轨道半径分别为r星、r船,周期分别为T星、T船,且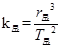 ,
,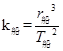 ,则下列说法或结果正确的是( )
,则下列说法或结果正确的是( )
| A.“神舟七号”绕地运行的速率大于7.9 km/s |
| B.“嫦娥一号”绕月运行的速率为3.95 km/s |
| C.k星∶k船=1∶81 |
| D.T星∶T船=1∶4 |