题目内容
9.设想未来人类登上了火星,有一兴趣小组用如图1所示的实验装置验证m1、m2组成的系统在火星上机械能是否守恒.m2从高处由静止开始下落,m1上拖着的纸带打出一系列的点,对纸带上的点迹进行测量,即可验证机械能守恒定律.若如图2给出的是实验中获取的一条纸带:0是打下的第一个点,每相邻两计数点间还有4个点(图中未标出),计数点间的距离如图所示.已知m1=50g、m2=150g,则(结果均保留两位有效数字)
(1)打点5时的速度=2.4 m/s;物体运动的加速度=4.8 m/s2;
(2)物体m2由静止开始下落h时的速度为v,火星的重力加速度g如果等式(m2-m1)gh=$\frac{1}{2}$(m1+m2)v2成立(用给出的字母表示),即可验证m1、m2组成的系统机械能守恒.
(3)若该兴趣小组作出$\frac{1}{2}$v2-h图象如图3所示,则火星的重力加速度g=4.0m/s2.
分析 纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,
由速度,可求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
对于物理量线性关系图象的应用我们要从两方面:1、从物理角度找出两变量之间的关系式;
2、从数学角度找出图象的截距和斜率,两方面结合解决问题.
解答 解:(1)利用匀变速直线运动的推论有:
v5=$\frac{{x}_{46}}{{t}_{46}}$=$\frac{0.216+0.264}{0.2}$=2.4m/s;
根据$a=\frac{△x}{{T}^{2}}$=$\frac{0.264-0.216}{0.{1}^{2}}$=4.8m/s2;
(2)系统动能的增量为:△EK=$\frac{1}{2}$(m1+m2)v2.
系统重力势能减小量为:△Ep=(m2-m1)gh
当$\frac{1}{2}$(m1+m2)v2=(m2-m1)gh时,则m1、m2组成的系统机械能守恒;
(3)由于$\frac{1}{2}$(m1+m2)v2=(m2-m1)gh
得到:$\frac{1}{2}$v2=$\frac{g}{2}$h
所以$\frac{1}{2}$v2-h图象的斜率k=$\frac{g}{2}$=$\frac{2.4}{1.2}$=2
因此g=4.0m/s2.
故答案为:(1)2.4,4.8;(2)(m2-m1)gh=$\frac{1}{2}$(m1+m2)v2;(3)4.0.
点评 该题的研究对象是系统,要注意m1和m2的重力势能的变化情况.
利用$\frac{1}{2}$v2-h图线处理数据,(m1+m2)=2(m2-m1),那么$\frac{1}{2}$v2-h图线的斜率就等于$\frac{g}{2}$.
直线图象中斜率和截距是我们能够利用的信息.

| A. | 经过相等位移,a、b两物体动能增加量不同 | |
| B. | 经过相等时间,a、b两物体速度增加量相同 | |
| C. | 运动过程中,a、b两物体速度之差与时间成正比 | |
| D. | 运动过程中,a、b两物体位移之差与时间成正比 |
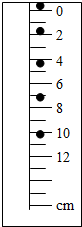
 如图所示是某同学测量匀变速直线运动的加速度时,从若干纸带中选中的一条纸带的一部分,他每隔4个点取一个计数点,图上注明了他对各计数点间距离的测量结果.
如图所示是某同学测量匀变速直线运动的加速度时,从若干纸带中选中的一条纸带的一部分,他每隔4个点取一个计数点,图上注明了他对各计数点间距离的测量结果.(1)为了验证小车的运动是匀变速运动,请进行下列计算,填入表内(单位:cm).
| x2-x1 | x3-x2 | x4-x3 | x5-x4 | x6-x5 | $\overline{△x}$ |
| 1.60 | 1.55 | 1.62 | 1.53 | 1.61 | 1.88 |
(2)根据匀变速直线运动的规律,可以求得物体的加速度$\overline{α}$=1.58m/s2.(计算结果保留三位有效数字).
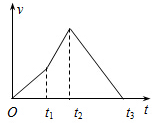 某科技兴趣小组用实验装置来模拟火箭发射卫星.火箭点燃后从地面竖直升空,t1时刻第一级火箭燃料燃尽后脱落,t2时刻第二级火箭燃料燃尽后脱落,此后不再有燃料燃烧.实验中测得火箭竖直方向的速度-时间图象如图所示,设运动中不计空气阻力,燃料燃烧时产生的推力大小恒定.下列判断正确的是( )
某科技兴趣小组用实验装置来模拟火箭发射卫星.火箭点燃后从地面竖直升空,t1时刻第一级火箭燃料燃尽后脱落,t2时刻第二级火箭燃料燃尽后脱落,此后不再有燃料燃烧.实验中测得火箭竖直方向的速度-时间图象如图所示,设运动中不计空气阻力,燃料燃烧时产生的推力大小恒定.下列判断正确的是( )| A. | t2时刻火箭到达最高点,t3时刻火箭落回地面 | |
| B. | 火箭在0~t1时间内的加速度大于t1~t2时间内的加速度 | |
| C. | t3时刻火箭达到最高点 | |
| D. | 火箭在t2~t3时间内运动方向与0~t2时间内运动方向相反 |
 如图为一运动小球的仿“频闪”照片,频闪时间间隔为0.1s.
如图为一运动小球的仿“频闪”照片,频闪时间间隔为0.1s. 如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为UA=15V,UB=3V,UC=-3V,由此
如图所示,A、B、C、D是匀强电场中一正方形的四个顶点,已知A、B、C三点的电势分别为UA=15V,UB=3V,UC=-3V,由此



 甲、乙物体做直线运动,两物体的v-t图象如图所示,若它们的初速度的大小都为v0,末速度的大小都为v1,则在时间t1内甲物体的平均速度$\overline{{v}_{甲}}$=$\frac{{v}_{0}+{v}_{t}}{2}$,且$\overline{{v}_{甲}}$<$\overline{{v}_{乙}}$(选填“>”、“=”或“<”)
甲、乙物体做直线运动,两物体的v-t图象如图所示,若它们的初速度的大小都为v0,末速度的大小都为v1,则在时间t1内甲物体的平均速度$\overline{{v}_{甲}}$=$\frac{{v}_{0}+{v}_{t}}{2}$,且$\overline{{v}_{甲}}$<$\overline{{v}_{乙}}$(选填“>”、“=”或“<”)