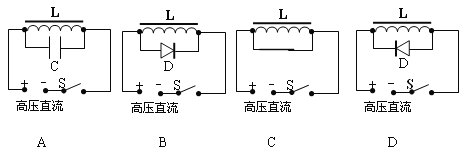
题目内容
【题目】如图所示，质量为m=0．2kg的小球（可视为质点）从水平桌面右端点A以初速度
水平抛出，桌面右侧有一竖直放置的光滑轨道MNP，其为半径R=0．8m的圆环剪去了左上角135°的圆弧，MN为其竖直直径，P点到桌面的竖直距离为R，小球飞离桌面后恰由P点无碰撞地落入圆轨道，取
。
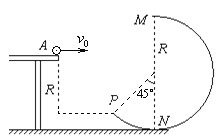
（1）求小球在A点的初速度
以及AP间的水平距离x；
（2）求小球到达圆轨道最低点N时对N点的压力；
（3）判断小球能否到达圆轨道最高点M。
【答案】（1）
（2）
（3）不能
【解析】
试题分析：（1）物块由A点做平抛运动，在P点恰好沿圆轨道的切线进入轨道，则物块在P点的竖直分速度为：
由平抛运动规律得：
代入数据解得：．
（2）物块在P点的速度为：
物块从P点到N点，由动能定理得：
物块在N点，由牛顿第二定律得：
代入数据解得物块所受支持力为：
由牛顿第三定律得，物块对N点的压力为
，方向竖直向下．
（3）假设小球能够到达M点，由功能关系得：
代入数据解得：
小球能够完成圆周运动，在M点须有：
，
即：
，由
知，小球不能到达圆轨道最高点M．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
