��Ŀ����
15��Ϊ�˲���С������ˮƽ�����Ķ�Ħ��������ijС���������ͼ����ʾ��ʵ��װ�ã����е���ɹ̶��������ϣ��ᵯ������뵲��������ͼ�������Ϊh��O1��O2��A��B��C����ͬһˮƽֱ���ϣ���֪�������ٶ�Ϊg�����������ɺ��Բ��ƣ�ʵ�����һ������̶���O1�㣬�ƶ�����ѹ�����ɣ������Ƶ�A��������O1A�ľ��룬��ͼ����ʾ�������ɾ�ֹ�ͷţ�����ˮƽ���ϵ�P�㣬���P�㵽�����Ҷ˵�ˮƽ����Ϊx1��
ʵ����̶���������Ĺ̶����Ƶ���O1�����Ϊd��O2�㣬��ͼ����ʾ���ƶ�����ѹ�����ɣ������Ƶ�C����ʹO2C�ľ�����O1A�ľ�����ȣ������ɾ�ֹ�ͷţ�����ˮƽ���ϵ�Q�㣬���Q�㵽�����Ҷ˵�ˮƽ����Ϊx2��

��1��Ϊ��ɱ�ʵ�飬����˵������ȷ����C
A��������С��������� B�����������ɵľ���ϵ�� C�����ɵ�ѹ��������̫С D�����������ɵ�ԭ��
��2��д����Ħ�������ı���ʽ��=$\frac{{x}_{1}^{2}-{x}_{2}^{2}}{4dh}$�������������������ķ��ű�ʾ��
��3��С���ڽ���ʵ����̶�ʱ�����ֻ���δ�ܻ������森Ϊ�˲���С������ˮƽ�����Ķ�Ħ������������������������ǻ���ֹͣ������λ�õ�B��ľ��룮
��4��ijͬѧ��Ϊ������������߶ȣ�����������С����ӷ������浽��ص�ʱ�䣬Ҳ�ɲ��С������ˮƽ�����Ķ�Ħ����������ʵ�鷽�������У�ѡ����С������С����������ǻ����ڿ��з���ʱ��̣ܶ������ռ�ʱ�����յ㣬�����ʱ�����ϴ�
���� ��ʵ������IJ����֪����������µ������Ĺ���ȣ���黬������ʱ�Ķ����ǵ���������Ħ���������ĺͣ�������黬����ͬ�����µ�Ħ�������Ĺ����������Ħ�����Ĵ�С��Ħ�������Ĵ�С
��� �⣺��1��2�������뿪�������ƽ���˶���ƽ���˶���ʱ�䣺t=$\sqrt{\frac{2h}{g}}$������еľ��룺x=v•t
���Ի����1���뿪����ʱ���ٶȣ�v1=x1•$\sqrt{\frac{g}{2h}}$��
�����2���뿪����ʱ���ٶȣ�v2=x2•$\sqrt{\frac{g}{2h}}$��
�����1�λ����Ĺ����У����ɵĵ�����Ħ�����������赯�����Ĺ���W1��AB֮��ľ�����x����W1-��mg•x=$\frac{1}{2}$m ${v}_{1}^{2}$��
�����1�λ����Ĺ����У�W1-��mg•��x+d�� ��
�����٢ڢۢܿɵã���mg•d=$\frac{1}{2}$m��${v}_{2}^{2}$-${v}_{1}^{2}$��
������=$\frac{{x}_{1}^{2}-{x}_{2}^{2}}{4dh}$
��֪��Ҫ�ⶨĦ���������뵯�ɵij��ȡ����ɵľ���ϵ�����Լ�������������أ�Ҫ���û���˳���������棬���ɵ�ѹ��������̫С����C��ȷ��
��ѡ��C
��3���ڽ���ʵ����̶�ʱ�����ֻ���δ�ܻ������棬�������Ϊ�����ĩ�ٶ���0��Ϊ�˲���С������ˮƽ�����Ķ�Ħ������������Ҫ����������ֹͣ������λ�õ�B��ľ��룮
��4������������С����ӷ������浽��ص�ʱ�䣬���ⶨС������ˮƽ�����Ķ�Ħ����������ʵ�鷽���Dz����еģ�ԭ���� �����ڿ��з���ʱ��̣ܶ������ռ�ʱ�����յ㣬�����ʱ�����ϴ�
�ʴ�Ϊ����1��C����2��$\frac{{x}_{1}^{2}-{x}_{2}^{2}}{4dh}$��
��3������ֹͣ������λ�õ�B��ľ��룻
��4�������У������ڿ��з���ʱ��̣ܶ������ռ�ʱ�����յ㣬�����ʱ�����ϴ�
���� ���⿼����̽��Ӱ��Ħ������С�����ؼ���Ħ�������IJⶨ�����ڿ��鿼����ʵ��ԭ����������������ݴ������������������Ӧ����ѧ�������ɽ��ʵ�������������

| A�� | �ʵ�4sĩ���ٶ�Ϊ10m/s | B�� | �ʵ�2sĩ���ٶ�Ϊ6m/s | ||
| C�� | �ʵ�4s�ڵ�ƽ���ٶ�Ϊ5m/s | D�� | �ʵ�ļ��ٶ�Ϊ3m/s2 |
| A�� | 1.5m/s | B�� | 3m/s | C�� | 3.5m/s | D�� | 4m/s |
 ������ͬλ��14C�ڿ���������ҪӦ�ã�Ϊ�о�14C��˥����ɣ���һ��ԭ����ֹ��14Cԭ�Ӻ˷�����ǿ�ų��У��۲쵽��������������뷴��˵ľ������������е�Բ��Բ�İ뾶֮��R��r=7��1����ͼ��ʾ����ô14C��˥�䷽��ʽӦ�ǣ�������
������ͬλ��14C�ڿ���������ҪӦ�ã�Ϊ�о�14C��˥����ɣ���һ��ԭ����ֹ��14Cԭ�Ӻ˷�����ǿ�ų��У��۲쵽��������������뷴��˵ľ������������е�Բ��Բ�İ뾶֮��R��r=7��1����ͼ��ʾ����ô14C��˥�䷽��ʽӦ�ǣ�������| A�� | ${\;}_{6}^{14}$C��${\;}_{4}^{10}$Be+${\;}_{2}^{4}$He | B�� | ${\;}_{6}^{14}$C��${\;}_{5}^{14}$B+${\;}_{1}^{0}$e | ||
| C�� | ${\;}_{6}^{14}$C��${\;}_{7}^{14}$N+${\;}_{-1}^{0}$e | D�� | ${\;}_{6}^{14}$C��${\;}_{5}^{12}$B+${\;}_{1}^{2}$H |
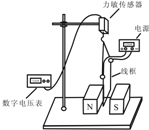 ������ͼ��ʾ��ʵ��װ�ÿ��Բ����Ÿ�Ӧǿ��B���þ�Ե����˿�߰ѵײ���ΪL������ΪR������Ϊm�ġ���?�����߿�̶��������������Ĺҹ��ϣ��������ʵ��������߿����Դ�����ߵĵ�����Բ��ƣ����������F�����������������Ĺҹ���ʱ�����ֵ�ѹ������ʾ��U�������ֵ�ѹ���ϵ�ʾ��U����������F�����ȣ���U=KF��ʽ��KΪ����ϵ�������߿����㶨��ѹΪE1ʱ����ѹ����ʾ��ΪU1������㶨��ѹΪE2ʱ���������䣩����ѹ��ʾ��ΪU2����Ÿ�Ӧǿ��B�Ĵ�СΪ��������
������ͼ��ʾ��ʵ��װ�ÿ��Բ����Ÿ�Ӧǿ��B���þ�Ե����˿�߰ѵײ���ΪL������ΪR������Ϊm�ġ���?�����߿�̶��������������Ĺҹ��ϣ��������ʵ��������߿����Դ�����ߵĵ�����Բ��ƣ����������F�����������������Ĺҹ���ʱ�����ֵ�ѹ������ʾ��U�������ֵ�ѹ���ϵ�ʾ��U����������F�����ȣ���U=KF��ʽ��KΪ����ϵ�������߿����㶨��ѹΪE1ʱ����ѹ����ʾ��ΪU1������㶨��ѹΪE2ʱ���������䣩����ѹ��ʾ��ΪU2����Ÿ�Ӧǿ��B�Ĵ�СΪ��������| A�� | B=$\frac{R��{U}_{1}-{U}_{2}��}{K��{E}_{1}-{E}_{2}��L}$ | B�� | B=$\frac{R��{U}_{1}-{U}_{2}��}{K��{E}_{1}+{E}_{2}��L}$ | ||
| C�� | B=$\frac{R��\sqrt{{U}_{1}}-\sqrt{{U}_{2}}��}{\sqrt{K}��{E}_{1}-{E}_{2}��L}$ | D�� | B=$\frac{R��\sqrt{{U}_{1}}-\sqrt{{U}_{2}}��}{\sqrt{K}��{E}_{1}+{E}_{2}��L}$ |
| A�� | A��ĵ���Ϊ4V | |
| B�� | �����B��ĵ�����Ϊ4��10-6J | |
| C�� | ��ɴ�D�Ƶ�B�˷��糡������4��10-6J | |
| D�� | C��A�����Ʋ�UCAΪ5V |
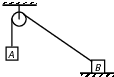 ��ͼ��ʾ��������A��Bͨ����������ֵ���������������B��ֹ��ˮƽ�����ϣ����ƻ��ִ���Ħ������������˵������ȷ���ǣ�������
��ͼ��ʾ��������A��Bͨ����������ֵ���������������B��ֹ��ˮƽ�����ϣ����ƻ��ִ���Ħ������������˵������ȷ���ǣ�������| A�� | ����B��������С����A��������С | B�� | B�Ե����ѹ��һ����Ϊ�� | ||
| C�� | B�ܵ������Ħ��������Ϊ�� | D�� | A������һ��С��B������ |
 �����������裬����������G1����r1�ĵ�·��ͼ1��ʾ����ѡ����������£�
�����������裬����������G1����r1�ĵ�·��ͼ1��ʾ����ѡ����������£�