��Ŀ����
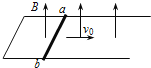
����Ŀ����ͼ��ʾ�����Ϊ����б��A���̶���ˮƽ���ϣ�ϸ�ߵ�һ�˹̶���ǽ�棬��һ�˿��б�涥�˵�С���������B������B��ֹ��б���ϣ���������ϸ��ˮƽ���Ҳ��ϸ����б��ƽ�У�A��B��������Ϊm.��ȥ�̶�A��װ�ú�A��B����ֱ���˶�������һ��Ħ�����������ٶ�Ϊg.��

(1)A�̶�����ʱ��A��B֧�����Ĵ�СN��
(2)A������λ��Ϊxʱ��B��λ�ƴ�Сs��
(3)A������λ��Ϊxʱ���ٶȴ�СvA.
���𰸡�(1) ![]() (2)
(2) ![]() ��(3)
��(3) ![]()
��������
���⣨1��֧�����Ĵ�СN=" mgcos" ��
��2�����ݼ��ι�ϵsx=x����1-cos����, sy=x��sin��
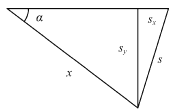
��s=![]()
���s=![]()
��3��B���½��߶�sy=x��sin��
���ݻ�е���غ㶨��mgsy=![]() mvA2+
mvA2+![]() mvB2
mvB2
�����ٶȵĶ����vA=![]() ��vB=
��vB=![]()
��![]()
���vA=![]() ��
��
�ⷨ����
��2��B�����A��б���»��������λ����б�淽���ɣ�![]() ����λ�ƹ�ϵ��ͼ��ʾ
����λ�ƹ�ϵ��ͼ��ʾ

��A��б���»�λ�ƴ�С���������ı仯����ͼ��
![]()
����![]()
��3����![]() ���ٶȵĹ�ϵ��λ�ƹ�ϵ��ͬ����
���ٶȵĹ�ϵ��λ�ƹ�ϵ��ͬ����![]()
���ݻ�е���غ㶨��mg x��sin��=![]() mvA2+
mvA2+![]() mvB2
mvB2
��֮vA=![]()

��ϰ��ϵ�д�
�����Ŀ