题目内容
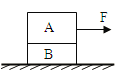
【题目】如图所示,质量为mB=1.5kg的小平板车B静止在光滑水平面上,车的左端静止着质量为mA=450g的物块A(可视为质点),物块A与平板车上板面的动摩擦因数μ=0.1,一个质量为m0=50g的子弹以10m/s的水平速度瞬间射入A并留在其中.若使物块A不从平板车上滑出,试求:(g取10m/s2)
①平板车的最小长度是多少?
②物块A在平板车上相对于平板车滑行的时间是多少?
【答案】解:①子弹射入物体A并留在A中,规定向右为正方向,运用动量守恒定律得:
m0v0=(m0+mA)vA
代入数据得子弹和A的共同速度为:vA=1m/s
子弹和A在车上滑行,对A、B组成的系统研究,根据动量守恒定律得:
(m0+mA)vA=(m0+mA+mB)v
代入数据得最终A和车B速度共同速度:v=0.25m/s
根据能量守恒定律得物体A与平板车间因摩擦产生的热量等于该过程的动能减小量,有:
Q=μmgd= ![]() (m0+mA)vA2﹣
(m0+mA)vA2﹣ ![]() (m0+mA+mB)v2
(m0+mA+mB)v2
代入数据得:d= ![]() m
m
所以平板车的最小长度是 ![]() m.
m.
②对于平板车,由动量定理得:
μmgt=mBv﹣0
解得,A在平板车上相对于平板车滑行的时间为:t=0.75s
答:①平板车的最小长度是 ![]() m.
m.
②物块A在平板车上相对于平板车滑行的时间是0.75s.
【解析】①子弹射入物体A并留在A中,子弹和A组成的系统动量守恒,由动量守恒定律可以求出两者共同速度.物块A不从平板车上滑出时,速度与平板车相同.由系统的动量守恒求三者共同速度,再由能量守恒定律可以求出A相对于平板车滑行的距离,即为平板车的最小长度.②对平板车,运用动量定理求滑行时间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目