题目内容
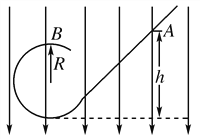
【题目】两条相距为L的平行光滑导轨（足够长）ab与cd，倾角为θ，阻值为R的电阻与导轨的a、c端相连。质量为m、电阻也为R的导体棒垂直于导轨放置并可沿导轨自由滑动。整个装置放于匀强磁场中，磁场的方向垂直导轨平面向上，磁感应强度的大小为B．导体棒的中点系一不可伸长的轻绳，绳绕过固定在桌边的光滑轻滑轮后，与一个质量也为m的物块相连，绳处于拉直状态且与斜面平行。现从静止开始释放物块，物块下落高度为h速度恰好达到最大（物块不会触地），已知重力加速度为g，其他电阻不计。求：
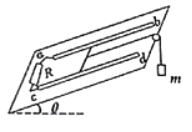
（1）物块下落的最大速度；
（2）从初始到物块速度最大过程中，通过电阻R的电荷量；
（3）若物块下落到最大速度时剪断细绳，之后导体棒上升的最大距离为x，求在此运动过程中R上产生的焦耳热。
【答案】（1）
（2）
（3）
【解析】
（1）物体下落达到最大速度vm时，导体棒处于平衡状态：mg＝mgsinθ+F
导体棒所受安培力为：F＝BIL
导体棒的电流为：
联立解得：
（2）通过电阻R的电荷量为：
（3）在此运动过程中R和导体棒上产生的焦耳热相等，设为Q，根据能量守恒有：
解得：
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
