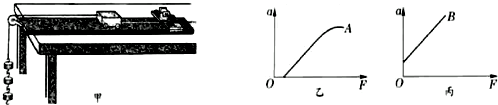题目内容
如图19所示,有一行星探测器,质量为1
图19
(1)该行星表面附近的重力加速度的大小;?
(2)发动机正常工作时的推力.
g=
解析:(1)由题意可知,9 s末发动机关闭,探测器只受重力作用,故它在这一阶段的加速度即为该行星表面的重力加速度.由图线的斜率可知g=64/16 m/s2=
(2)在0-9 s内,探测器受到竖直向上推力F和竖直向下的重力G.?
由图线的斜率可知这一阶段的加速度a=64/9 m/s2.?
由牛顿第二定律F-mg=ma?
得F=m(g+a)=2 000 N.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

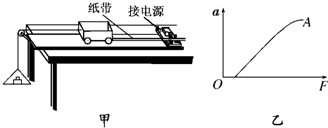
 一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图所示)、小车、计时器一个、米尺.请填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):
一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图所示)、小车、计时器一个、米尺.请填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):