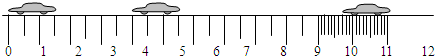题目内容
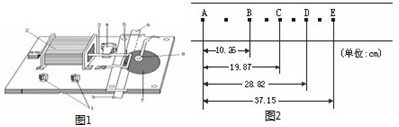
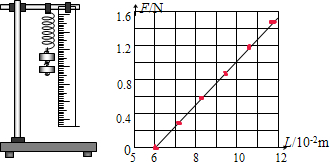
(Ⅰ)(6分)某同学在做探究弹力和弹簧伸长的关系的实验中,设计了如图所示的实验装置.所用的钩码每只的质量都是30g,他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中.(弹力始终未超过弹性限度,取g=10m/s2)
①试根据这些实验数据在右图给定的坐标纸上作出弹簧所受弹力大小F跟弹簧总长L之间的函数关系图线.
②该弹簧的劲度系数k=
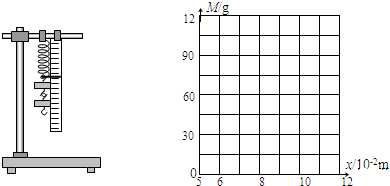
(Ⅱ)(1)现要验证“当质量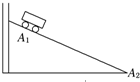 一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图所示)、小车、计时器一个、米尺.请填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):
一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图所示)、小车、计时器一个、米尺.请填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):
①让小车自斜面上方一固定点A1从静止开始下滑至斜面底端A2,记下所用的时间t.
②用米尺测量A1与A2之间的距离x,则小车的加速度a=
.
③用米尺测量A1相对于A2的高度h.设小车所受重力为mg,则小车所受合外力F=
④改变
⑤以h为横坐标,1/t2为纵坐标,根据实验数据作图.如能得到一条过原点的直线,则可以验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一规律.
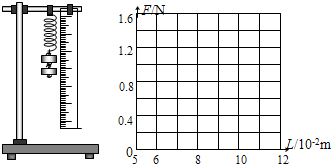
(2)在“验证牛顿运动定律”的实验中,实验装置如图甲所示,有一位同学通过实验测量作出了图乙中的A图线.试分析:
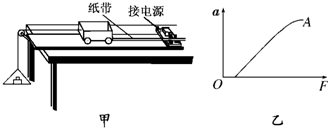
①A图线不通过坐标原点的原因是
②A图线上部弯曲的原因是
| 砝码质量(g) | 0 | 30 | 60 | 90 | 120 | 150 |
| 弹簧总长(cm) | 6.00 | 7.15 | 8.34 | 9.48 | 10.64 | 11.79 |
| 弹力大小(N) | 0 | 0.3 | 0.6 | 0.9 | 1.2 | 1.5 |

①试根据这些实验数据在右图给定的坐标纸上作出弹簧所受弹力大小F跟弹簧总长L之间的函数关系图线.
②该弹簧的劲度系数k=
25N/m
25N/m
(Ⅱ)(1)现要验证“当质量
 一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图所示)、小车、计时器一个、米尺.请填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):
一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:一倾角可以调节的长斜面(如图所示)、小车、计时器一个、米尺.请填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):①让小车自斜面上方一固定点A1从静止开始下滑至斜面底端A2,记下所用的时间t.
②用米尺测量A1与A2之间的距离x,则小车的加速度a=
| 2x |
| t2 |
| 2x |
| t2 |
③用米尺测量A1相对于A2的高度h.设小车所受重力为mg,则小车所受合外力F=
mg
| h |
| x |
mg
.| h |
| x |
④改变
斜面倾角(或h的数值)
斜面倾角(或h的数值)
,重复上述测量.⑤以h为横坐标,1/t2为纵坐标,根据实验数据作图.如能得到一条过原点的直线,则可以验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一规律.
(2)在“验证牛顿运动定律”的实验中,实验装置如图甲所示,有一位同学通过实验测量作出了图乙中的A图线.试分析:

①A图线不通过坐标原点的原因是
没有平衡摩擦力或平衡摩擦力不够
没有平衡摩擦力或平衡摩擦力不够
;②A图线上部弯曲的原因是
未满足钩码质量远小于小车质量
未满足钩码质量远小于小车质量
.分析:(1)由胡克定律:F=kx得:弹力F和形变量x是正比关系,图线应是过原点的直线,作图时不在图线上的点要舍弃,做出的图线的斜率即是劲度系数k.
(2)小车做的是初速度为零的匀加速直线运动,根据运动规律:s=
at2可求出加速度a;小车所受的合外力是重力沿斜面的分力,大小为:mgsinθ,θ为斜面的夹角,求出sinθ,即可求出合外力F;用动能定理可解得:h=
,所以h与
成正比,所以我们需要改变h.
(3)根据牛顿第二定律和图象的特点可分析实验实验误差产生的原因.
(2)小车做的是初速度为零的匀加速直线运动,根据运动规律:s=
| 1 |
| 2 |
| 2s2 |
| gt2 |
| 1 |
| t2 |
(3)根据牛顿第二定律和图象的特点可分析实验实验误差产生的原因.
解答:(1)解:(1)根据实验数据在坐标纸上描出的点,基本上在同一条直线上.可以判定F和L间是一次函数关系.画一条直线,使尽可能多的点落在这条直线上,不在直线上的点均匀地分布在直线两侧.
②由k=
可得:k=25N/m.
(2)①小车做的是初速度为零的匀加速直线运动,根据运动规律:x=
at2,解得:a=
②小车所受的合外力是重力沿斜面的分力,大小为:mgsinθ,θ为斜面的夹角,sinθ=
=
,所以合力为:F=mgsinθ=
.
③用动能定理可解得:h=
,所以h与
成正比,所以我们需要改变h,所以需要:改变斜面的倾角或斜面高h
(3)①由图象可知,当小车所受拉力不为零时,加速度仍然没有产生,因此该实验的操作不当为:没有平衡摩擦力或平衡摩擦力不够.
②设小车与砝码的质量为M,小桶与砂子的质量为m,根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
当m<<M时,绳子的拉力近似等于砂和砂桶的总重力.当小桶与砂子的质量为m变大后不能满足m<<M的条件,故图象弯曲,故应填:未满足钩码质量远小于小车质量.
故答案为:(1)①见上图;②25N/m
(2)②
;③
;④改变斜面的倾角或斜面高h
(3)①没有平衡摩擦力或平衡摩擦力不够;②未满足钩码质量远小于小车质量.

②由k=
| △F |
| △x |
(2)①小车做的是初速度为零的匀加速直线运动,根据运动规律:x=
| 1 |
| 2 |
| 2x |
| t2 |
②小车所受的合外力是重力沿斜面的分力,大小为:mgsinθ,θ为斜面的夹角,sinθ=
| 对边 |
| 斜边 |
| h |
| x |
| mgh |
| x |
③用动能定理可解得:h=
| 2x2 |
| gt2 |
| 1 |
| t2 |
(3)①由图象可知,当小车所受拉力不为零时,加速度仍然没有产生,因此该实验的操作不当为:没有平衡摩擦力或平衡摩擦力不够.
②设小车与砝码的质量为M,小桶与砂子的质量为m,根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
| mMg |
| M+m |
当m<<M时,绳子的拉力近似等于砂和砂桶的总重力.当小桶与砂子的质量为m变大后不能满足m<<M的条件,故图象弯曲,故应填:未满足钩码质量远小于小车质量.
故答案为:(1)①见上图;②25N/m
(2)②
| 2x |
| t2 |
| mgh |
| x |
(3)①没有平衡摩擦力或平衡摩擦力不够;②未满足钩码质量远小于小车质量.
点评:(1)第一题比较简单考查了胡可定律的应用,做题时需要结合数学知识求解,是一道考查数学与物理结合的好题目.
(2)第二题的关键是找出实验原理,是重力沿斜面的分力做为合外力,最终得到h=
,h与
成正比,来对实验数据进行分析.
(3)解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项.其中平衡摩擦力的原因以及做法在实验中应当清楚.
(2)第二题的关键是找出实验原理,是重力沿斜面的分力做为合外力,最终得到h=
| 2s2 |
| gt2 |
| 1 |
| t2 |
(3)解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项.其中平衡摩擦力的原因以及做法在实验中应当清楚.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

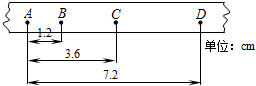 某同学在做“探究小车速度随时间变化的规律”实验时,得到了如图一条较为理想的纸带,从某点开始,已在纸带上每隔0.1s取好一个计数点,即两计数点之间的时间间隔为0.1s,依打点先后编为A、B、C、D如图所示,测出AB=1.2cm,AC=3.6cm,AD=7.2cm,则打B点时小车的瞬时速度vB=
某同学在做“探究小车速度随时间变化的规律”实验时,得到了如图一条较为理想的纸带,从某点开始,已在纸带上每隔0.1s取好一个计数点,即两计数点之间的时间间隔为0.1s,依打点先后编为A、B、C、D如图所示,测出AB=1.2cm,AC=3.6cm,AD=7.2cm,则打B点时小车的瞬时速度vB=