题目内容
(1)如图甲所示为一列沿x轴正向传播的简谐横波在t=0时刻的图象,振源周期为1s.以下说法正确的是(仅有一个正确选项)
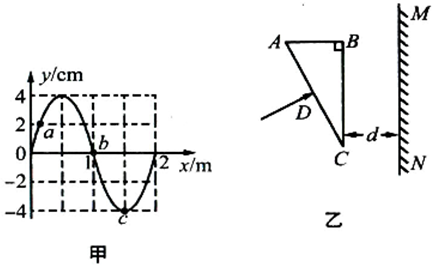
A.质点b的振幅为0
B.经过0.25s,质点b沿x轴正向移动0.5m
C.从t=0时刻起,质点c比质点a先回到平衡位置
D.在t=0时刻,质点a、c所受的回复力大小之比为1:2
(2)如图乙所示.有一截面是直角三角形的棱镜ABC,∠C=30°.在距BC边d处有一与BC边平行的光屏MN.现有某一单色光束从AC边的中点D垂直AC边射入棱镜.已知棱镜对该单色光折射率为n=
,光在真空中的传播速度为c.求该光束从BC边第一次出射到达MN的时间.

A.质点b的振幅为0
B.经过0.25s,质点b沿x轴正向移动0.5m
C.从t=0时刻起,质点c比质点a先回到平衡位置
D.在t=0时刻,质点a、c所受的回复力大小之比为1:2
(2)如图乙所示.有一截面是直角三角形的棱镜ABC,∠C=30°.在距BC边d处有一与BC边平行的光屏MN.现有某一单色光束从AC边的中点D垂直AC边射入棱镜.已知棱镜对该单色光折射率为n=
| 3 |
分析:(1)解答本题应抓住:简谐波传播过程中介质中各质点的振幅都相等;质点并不随波迁移;由波的传播方向判断质点的振动方向,即可判断质点c与质点a回到平衡位置的先后.质点做简谐运动,回复力F=-kx.
(2)根据几何关系求出在BC边上的入射角,通过折射定律求出在BC边上的折射角,根据几何关系求出从BC边第一次到达MN的距离,通过光速求出BC边第一次出射到达MN的时间.
(2)根据几何关系求出在BC边上的入射角,通过折射定律求出在BC边上的折射角,根据几何关系求出从BC边第一次到达MN的距离,通过光速求出BC边第一次出射到达MN的时间.
解答: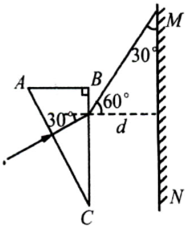 解:(1)A、图示时刻质点b的位移为0,但简谐波的每个质点的振幅都是相同的,其振幅为4cm,故A错误.
解:(1)A、图示时刻质点b的位移为0,但简谐波的每个质点的振幅都是相同的,其振幅为4cm,故A错误.
B、简谐横波沿x轴正向传播时,质点b只在自己平衡位置附近上下振动,并不向前移动.故B错误.
C、简谐横波沿x轴正向传播,t=0时刻.质点a正向下运动,回到平衡位置的时间小于
T,而质点c正向上运动,回到平衡位置的时间等于
T,故质点a比质点c先回到平衡位置.故C错误.
D、根据简谐运动的特征:F=-kx可知,在t=0时刻,质点a、c所受的回复力大小之比为1:2.故D正确.
故选D
(2)光从BC边射出时出射角为θ,n=
得 θ=60°
由几何关系知,光从BC边射出到达屏MN的路程为2d.
光从BC到达MN经历的时间t=
.
故答案为:
(1)D;(2)光束从BC边第一次出射到达MN的时间是
 解:(1)A、图示时刻质点b的位移为0,但简谐波的每个质点的振幅都是相同的,其振幅为4cm,故A错误.
解:(1)A、图示时刻质点b的位移为0,但简谐波的每个质点的振幅都是相同的,其振幅为4cm,故A错误.B、简谐横波沿x轴正向传播时,质点b只在自己平衡位置附近上下振动,并不向前移动.故B错误.
C、简谐横波沿x轴正向传播,t=0时刻.质点a正向下运动,回到平衡位置的时间小于
| 1 |
| 4 |
| 1 |
| 4 |
D、根据简谐运动的特征:F=-kx可知,在t=0时刻,质点a、c所受的回复力大小之比为1:2.故D正确.
故选D
(2)光从BC边射出时出射角为θ,n=
| sinθ |
| sin30° |
得 θ=60°
由几何关系知,光从BC边射出到达屏MN的路程为2d.
光从BC到达MN经历的时间t=
| 2d |
| c |
故答案为:
(1)D;(2)光束从BC边第一次出射到达MN的时间是
| 2d |
| c |
点评:第1题考查了波的基本特点:简谐波中各质点的振幅都相同、不“随波逐流”.
第2题考查几何光学问题,关键掌握光的折射定律.
第2题考查几何光学问题,关键掌握光的折射定律.

练习册系列答案
相关题目
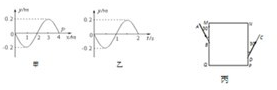 【物理-选修3-4】
【物理-选修3-4】
 (1)如图甲所示为一拉力传感器,某实验小组在用拉力传感器探究作用力与反作用力关系的实验中,获得了如图乙所示的图线.根据这个图线,你可以得出的结论是:
(1)如图甲所示为一拉力传感器,某实验小组在用拉力传感器探究作用力与反作用力关系的实验中,获得了如图乙所示的图线.根据这个图线,你可以得出的结论是: