题目内容
(9分)如图甲所示,相距为L的两平行金属导轨MN、PQ固定在绝缘水平面上,处于竖直向上的匀强磁场中,磁场的磁感应强度为B,导轨足够长且电阻不计.两根相同的金属棒c和d与导轨垂直放置,它们的质量均为m,电阻均为R,间距为s0,与导轨间的动摩擦因数均为μ,设最大静摩擦力与滑动摩擦力相等.在t=0时刻,对c棒施加一水平向右的力,使其从静止开始做匀加速直线运动.在t0时刻,d棒开始运动,此后保持水平力不变,由速度传感器测得两金属棒的v-t图象如图乙所示,从t1时刻开始两金属棒以相同的加速度做匀加速直线运动,此时两金属棒的间距为s,试求: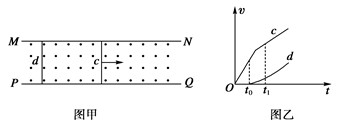
(1)在0至t1时间内通过金属棒c的电荷量;
(2)t0时刻回路的电功率和金属棒c的速度大小;
(3)t1时刻两金属棒的加速度大小.
(1) 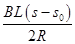 (2)
(2) 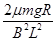 (3)
(3) 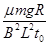
解析试题分析:(1)在0至t1这段时间内I=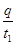 在
在
又I=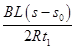
解得:q=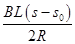
(2)设在t0时刻回路的瞬时感应电流为I,则对金属棒d由平衡条件得:BIL=μmg
t0时刻回路的电功率P=I2·2R
解得:P=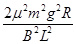
由欧姆定律得:I=
解得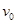 =
=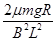
(3)设在t0时刻,水平外力为F0,金属棒c的加速度为a0,由牛顿第二定律得:F0-μmg-BIL=ma0
而a0=
从t1时刻起,对两金属棒组成的系统,由牛顿第二定律有F0-2μmg=2ma
解得:a=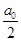 =
=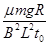
考点:本题考查了导体棒切割磁感线运动,以及牛顿第二定律的应用
点评:解决本题的关键会根据牛顿第二定律求加速度,以及结合运动学能够分析出金属棒的运动情况,

(1)(7分)利用如图甲所示装置探究动能定理,在固定斜面上有一质量为l kg的物块,后面固定一条穿过打点计时器的纸带。先接通电源,待打点稳定后,让物块从静止开始沿斜面匀加速下滑,得到一条如图乙所示的纸带。O点为打出的第二个点,A、B、C、D、E、F、G是计数点,每相邻两计数点间还有4个点未画出,各点间距如图所示,根据相关数据进行下列处理。(打点计时器的打点频率为50Hz,g =" 10" m/s2)

通过传感器测得物体所受的合外力是3.0 N。试完成下表:
| 从O点到各点过程合力所做的功W/J | 各点的动能Ek/J | ||
| OB | 0.8838 | B | 0.8845 |
| OC | 1.3275 | C | 1.3276 |
| OD | ? | D | 1.8634 |
| OE | 2.4858 | E | 2.4865 |
| OF | 3.1998 | F | ? |
(2)(6分)图1为某一热敏电阻(电阻值随温度的改变而改变,且对温度很敏感)的I – U关系曲线图。通过测量得到图1所示I – U关系的完整曲线,已知电源电动势恒为9 V(内阻不计),滑动变阻器的阻值为0 – 100 Ω,电压表V的内阻约为2 kΩ,电流表A的内阻约为0.2 Ω,热敏电阻的符号为


①请在虚线框内画出实验电路原理图。
②由题中给出的电源、热敏电阻、电流表和定值电阻R1组成如图2所示电路,电流表读数为30 mA。由热敏电阻的I – U关系曲线可知,热敏电阻两端的电压为 V;电阻R1的阻值为 Ω

(1)(7分)利用如图甲所示装置探究动能定理,在固定斜面上有一质量为l kg的物块,后面固定一条穿过打点计时器的纸带。先接通电源,待打点稳定后,让物块从静止开始沿斜面匀加速下滑,得到一条如图乙所示的纸带。O点为打出的第二个点,A、B、C、D、E、F、G是计数点,每相邻两计数点间还有4个点未画出,各点间距如图所示,根据相关数据进行下列处理。(打点计时器的打点频率为50Hz,g =" 10" m/s2)


通过传感器测得物体所受的合外力是3.0 N。试完成下表:
|
从O点到各点过程合力所做的功W/J |
各点的动能Ek/J |
||
|
OB |
0.8838 |
B |
0.8845 |
|
OC |
1.3275 |
C |
1.3276 |
|
OD |
? |
D |
1.8634 |
|
OE |
2.4858 |
E |
2.4865 |
|
OF |
3.1998 |
F |
? |
②根据①表中的数据,实验结论是 .
(2)(6分)图1为某一热敏电阻(电阻值随温度的改变而改变,且对温度很敏感)的I – U关系曲线图。通过测量得到图1所示I – U关系的完整曲线,已知电源电动势恒为9
V(内阻不计),滑动变阻器的阻值为0 –
100 Ω,电压表V的内阻约为2 kΩ,电流表A的内阻约为0.2 Ω,热敏电阻的符号为

①请在虚线框内画出实验电路原理图。
②由题中给出的电源、热敏电阻、电流表和定值电阻R1组成如图2所示电路,电流表读数为30 mA。由热敏电阻的I – U关系曲线可知,热敏电阻两端的电压为 V;电阻R1的阻值为 Ω
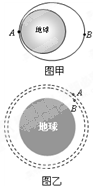 2011年9月29日21时16分,在酒泉卫星发射中心我国首个空间实验室“天宫一号”顺利发射升空,卫星的发射轨道为一椭圆,如图甲所示,地球的球心位于该椭圆的一个焦点上,A、B两点分别是卫星运行轨道上的近地点和远地点.若A点在地面附近,且卫星所受阻力可以忽略不计.“天宫一号”目标飞行器将和11月发射的“神舟八号”飞船实现对接,如乙图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由以上信息,可以判定( )
2011年9月29日21时16分,在酒泉卫星发射中心我国首个空间实验室“天宫一号”顺利发射升空,卫星的发射轨道为一椭圆,如图甲所示,地球的球心位于该椭圆的一个焦点上,A、B两点分别是卫星运行轨道上的近地点和远地点.若A点在地面附近,且卫星所受阻力可以忽略不计.“天宫一号”目标飞行器将和11月发射的“神舟八号”飞船实现对接,如乙图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由以上信息,可以判定( )


