Question

【题目】如图所示为一种获得高能粒子的装置----环形加速器，环形区域内存在垂直纸面向外的匀强磁场，质量为m、电荷量为+q的粒子在环中做半径为R的圆周运动，A、B为两块中心开有小孔的极板，原来电势都为零，每当粒子飞经A板时，A板电势升高为+U，B板电势仍保持为零，粒子在两极板间的电场中加速，每当粒子离开电场区域时，A板电势又降为零，粒子在电场一次次加速下动能不断增大，而在环形区域内绕半径不变（设极板间距远小于R），粒子重力不计，下列关于环形加速器的说法中正确的是

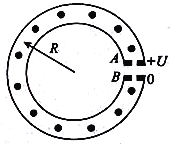
A. 加速器对带正电粒子顺时针加速，对待负电粒子加速需要升高B板电势

B. 电势U越高，粒子最终的速度就越大

C. 环形区域内的磁感应强度大小与加速次数n之间的关系为

D. 粒子每次绕行一圈所需的时间与加速次数n之间的关系为

Answer 1

【答案】C

【解析】带正电粒子从A板向B板加速，所以正电粒子沿顺时针运动，对负电粒子，若升高B板电势，则负电粒子从A板向B板加速，沿顺时针方向运动，但在磁场中洛伦兹力向外，无法提供向心力，A错误；根据可得，因为R是定值，最终速度由磁感应强度决定，B错误；粒子绕行n圈获得的动能等于电场力对粒子做的功，设粒子绕行n圈获得的速度为，根据动能定理可得，解得，粒子在环形区域磁场中，受洛伦兹力作用做半径为R的匀速圆周运动，根据牛顿第二定律和向心力公式，则有，解得，所以，C正确；粒子绕行第n圈所需时间，所以，D错误。